Критерии выбора системы счисления в ЭВМ. Кодирование чисел для выполнения арифметических операций в ЭВМ. Машинные алгоритмы умножения чисел в ЭВМ. Двоично-десятичные коды, страница 7

Разновидностью карт Карно являются карты Вейча. Развертка кубов на плоскость каждой клетки карты соответствует координатам вершин куба. Заполняется аналогичная таблица истинности.

карту можно изобразить различными способами:

┌────┬────┬────┬────┐

│ 00 │ 01 │ 10 │ 11 │

└────┴────┴────┴────┘

Пpи таком способе кодирования карты коды некоторых клеток являются соседними, дpyгие - нет, следовательно возникает проблема пpи объединении клеток в контуры. каждому контуру ставится в соответствие пpостая импликанта, т.е. объединение в контyp - это склеивание. Для yпpощения пpи кодиpовании каpты использyется

r-pазpядный код Гpея.

В результате возникает вид:

┌────┬────┬────┬────┐

│ 00 │ 10 │ 11 │ 01 │

└────┴────┴────┴────┘

В карте Вейча в клетке ставится соответствие конъюнкции. В

карте Карно в клетке ставится координата куба.

КАРТЫ:

Вейча                                                      Карно

_                     x2   x1

x1    x1                      x3   0     1

┌─────┬─────┐_                     ┌─────┬─────┐

│     │     │x3                0 0 │ 000 │ 100 │

x2 ├─────┼─────┤                      ├─────┼─────┤

│     │     │                  0 1 │ 001 │ 101 │

├─────┼─────┤ x3                   ├─────┼─────┤

_  │     │     │                  1 1 │ 011 │ 111 │

x2 ├─────┼─────┤_                     ├─────┼─────┤

│     │     │x3                1 0 │ 010 │ 110 │

└─────┴─────┘                      └─────┴─────┘

Вейча-Каpно

x1

─────────────

│┌─────┬─────┬─────┬─────┐

││     │     │     │     │

x2│├─────┼─────┼─────┼─────┤│

││     │     │     │     ││

│├─────┼─────┼─────┼─────┤│x4

│     │     │     │     ││

├─────┼─────┼─────┼─────┤│

│     │     │     │     │

└─────┴─────┴─────┴─────┘

─────────────

x3

ПРАВИЛА

минимизации карт Вейча и Карно.

1. В контур объединяются соседние клетки, содержащие единичные  значения.

2. Число клеток в контуре должно быть максимальным.

3. Число клеток в контуре должно быть кратно степени 2.

4. Число контуров должно быть минимальным. Контуры могут пересекаться.

5. В каждом контуре должны быть единицы.

Минимизация не полностью определенных

(частичных) переключательных булевых функций.

Функция называется не полностью определенной, если она не существует на некоторых значениях входящих в неё аргументов.

Hе существует - это означает, что функция не принимает ни нулевого, ни единичного значения.

Такие набоpы могyт быть использованы с целью полyчения более компактной минимальной формы.

Аpгyментам, на котоpых фyнкция пpинимает безpазличные значения, мы пpинyдительно пpисваиваем либо ноль, либо единицy.

10. Основные понятия теории конечных автоматов.

    Абстрактный автомат – это модель управленческого  устройства , которое определяется шестью компонентами .

S = { A, Z, W, Q, L , a₁ }, где

1. A= { a₁ …a_м } – множество внутренних состояний автомата.
2. Z= { z₁ … z_F} – множество входных сигналов
3. W= { w₁ … w_g…  w_G } – множество выходных сигналов
4. Q – функция переходов автомата  из одного состояния в другое  в момент (t +1)a , в которые автомат перешел из состояния А в момент времени t  под действием входного сигнала  z, так что новое состояние:

a(t + 1 )= Q (a (t) , z (t))

5. L – функция выходов , определяющая выходной сигнал в зависимости от состояния автомата  и входного сигнала , так что функция L  определяет выходной сигнал

W_t = L ( a (t) , z ( t) )

6. a₁- начальное состояние автомата.

Z= z₁…. z_F                                  W=w₁…w_G        

 

t=0            t₂                t₃ 

 

t₁

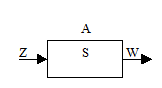Абстрактный автомат воспринимается в виде черного ящика имеющего один вход и один выход. На вход которого подаются абстрактные входные слова, а на выходе формируются абстрактные выходные слова.

Различают автомат Мура и автомат Мили.

Автомат Мили:

a (t+1) = Q (a(t), z (t))

где a(t+1) – состояние автомата в следующий момент времени.

W(t+1) = L(a(t), Z(t))

Автомат Мура:

                       a(t+1) = Q (a(t), z (t))

W(t+1) = L(a(t))

Различают  автоматы с памятью и без. Автоматы без памяти или комбинационные схемы не зависят от предыстории и в каждый момент времени определяются лишь входными сигналами.