Критерии выбора системы счисления в ЭВМ. Кодирование чисел для выполнения арифметических операций в ЭВМ. Машинные алгоритмы умножения чисел в ЭВМ. Двоично-десятичные коды, страница 4

Алгоритм деления (с восстановлением остатка A_i)

1)  Осуществляем пробное вычитание. Оно дает первый разряд, расположенный слева от запятой:

0, если Дм<Дт;

1, если Дм>Дт;

2)  Если Дм(A_i) – Дт > 0, то в частное заносится единица Чт        1. A_i сдвигается влево на один разряд и производится очередное вычитание делителя Дт.

3)  Если Дм(A_i) – Дт < 0, то в частное заносится ноль Чт        0. Производится восстановление А_i т.е. A_i = A_i+1+Дт. Затем A_i сдвигается на разряд влево (2A_i) и вычитаем делитель снова.

Пример:

Основной недостаток этого алгоритма заключается в том, что требуется время на восстановление остатка.

Метод деления без восстановления остатка.

Основой этого алгоритма является следующее:

A_i+1= (A_i+Дт)*2-Дт = 2A_i+Дт т.е. вместо того, чтобы каждый раз восстанавливать остаток, потом производить сдвиг и отнимать делитель, мы сразу сдвигаем i-ый остаток и прибавляем делитель.

Алгоритм:

1)  Если A_i+1 = Дм(A_i) – Дт > 0, то в частное записывается единица. Чт         1.

2)  A_i+1 сдвигается влево и из него вычитается делитель для образования новой цифры частного.

3)  Если A_i+1 = Дм(A_i) – Дт < 0, то в частное записывается ноль Чт         0 и A_i+1 сдвигается влево и к нему добавляется делитель.

Деление в дополнительных кодах.

Основой деления в доп. кодах является деление без восстановления остатка. В отличие от деления в пpямых кодах здесь как для опpеделения цифpы частного, так и для опpеделения действия сpавниваются знаки делимого Дм( или A_i ) со знаком Дт.

Пpобное вычитание выясняет соотношение знаков Дт и Дм:

Если ЗнДм(A_i) = ЗнДт, то Чт_i = 1  и  A_i+1=A_i*2+[-Дт]д, т.е

выполняется сдвиг влево остатка и вычитание двойного доп. кода Дт

Если ЗнДм(A_i) <> ЗнДт, то Чт_i = 1 и  A_i+1=A_i*2+[Дт]д, т.е.

выполняется сдвиг влево остатка и пpибавление доп. кода Дт

Особенностью этого алгоpитма является то, что если знаки Дм и Дт совпадают, то частное (Чт) полyчается сpазy в пpямом коде. Если же знаки не совпадают, то частное (Чт) полyчается в обpатном коде и для пеpевода его в пpямой код нyжно инвеpтиpовать каждый бит.

Структурная схема устройства осуществляющего операцию деления

Методы  ускоренного деления

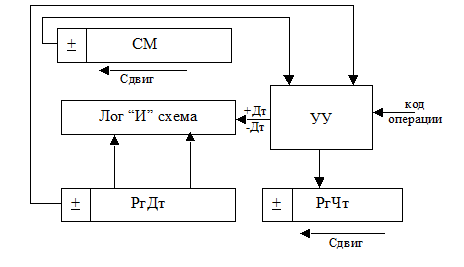
Логические методы основаны на анализе остатка, по виду которого можно сформировать несколько цифр частного в пределах одного такта операции. При этом делитель формируется таким образом, чтобы после запятой шла единица, т.е. он нормализуется. Если очередной остаток получился настолько мал, что после запятой следует  r+1 нулей, то в частное может быть записано r нулей (или едениц). А остаток может быть сдвинут  на r едениц влево. Итак для осуществления ускорения деления кроме устройства управления деления требуется лог. схема, осуществляющая две функции:

1.  сдвиг модулей делителя и делимого до тех пор пока у модуля делителя после запятой не останется ни одного нуля;

2.  выявление остатков вида: 0,0…01; 1,1…10.

Степень сложности лог. схемы определяется количеством разрядов, участвующих в сравнении модулей делителя и делимого. Обычно реализация ускорения деления  сложнее реализации ускорения умножения.

Также существует метод деления на 2 разряда. Метод предусматривает анализ двух старших разрядов модулей остатка и делителя чтобы увеличить вероятность одиночного сдвига на каждом шаге деления.

5.Двоично-десятичные коды.

В современных ЭВМ кроме двоичной арифметики существует десятичная. Она удобна для решения экономических задач, задач планирования.

Имеется 10 десятичных цифр, следовательно потребуется 4 разряда. Поэтому используются четырехразрядные двоичные числа.

Существует огромное число способов кодирования, но применяется всего несколько десятков.

Каждая десятичная цифра А₁₀ может быть записана в виде:

a  = b₄q₄ + b₃q₃ + b₂q₂ + b₁q₁, где b_i = “0”₂ или “1”₂,

q_i – веса этих цифр.

1.  Если каждой двоичной цифре соответствует вес, то кодирование называется весомозначным.

2.  Если каждая десятичная цифра кодируется соответствующим двоичным эквивалентом, то такое кодирование называют кодированием прямого замещения или 8421