x1x2; x1x2x3; x4
– элементарная конъюнкция.
x1x2; x1x2x3
– не элементарная конъюнкция
2. Элементарная конъюнкция является конъюнкцией ранга “n”, если в нее входит полный набор n переменных от которых зависит ПФ (переключательная функция).
f = x1x2x3x4
+ x1x2x3x4
ранг n ранг n
3. Дизъюнктивная нормальная форма(ДНФ) – дизъюнкция конечного числа элементарных конъюнкций.
f = x1x2x3 + x1x2
+x1 – ДНФ
4. Совершенная ДНФ (СДНФ) – дизъюнкция конечного множества элементарных конъюнкций ранга “n”.
f = x1x2x3x4
+ x1x2x3x4 + x1x2x3x4
5. Совершенная КНФ (СКНФ) – конъюнкция конечного множества элементарных дизъюнкций ранга “n”.
fскнф = Ф1 V xixi = (Ф1
V xi)( Ф1 V xi)
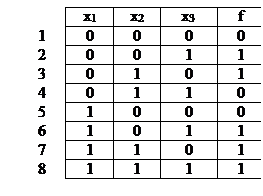
6. Если ПФ задана таблицей истинности, то она всегда записывается в СДНФ(или СКНФ).
Функция в СДНФ запишется по единичным значениям:
fсднф = x1x2x3
+ x1x2x3+ x1x2x3+
x1x2x3+ x1x2x3 (1)
функция в СКНФ запишется по нулевым значениям:
fскнф = (x1 +x2 + x3)
(x1 +x2 + x3) (x1 +x2 +
x3)
(2)
ПФ можно записать по нулевым значениям в форме СДНФ, т.к. при этом функция здесь принимает “0”, то поставим знак отрицания.
fсднф = x1x2x3
+ x1x2x3+ x1x2x3
К fсднф применим закон де Моргана:
 |
 |
 |
fсднф = x1x2x3 + x1x2x3+
x1x2x3
f
= (x1 +x2 + x3) (x1 + x2 +
x3 ) (x1 +x2 + x3 ) получена СКНФ
7. Простая импликанта - элементарная конъюнкция, которая не склеивается ни с какими другими элементарными конъюнкциями.
8. Сокращённая ДНФ - дизъюнкция простых импликант.
Для получения сокращенной формы правая часть исходной ПФ подвергается склеиванию
« n » шагов :
1 шаг : 1 конъюнкция склеивается со всеми ;
2 шаг : 2 1 конъюнкция склеивается со всеми.
В результате выполнения первого шага получим конъюнкции рангом на один меньше. На втором шаге производится склеивание конъюнкций ранга ”n-1” и т. д. Эти шаги повторяются до тех пор, пока не образуются простые импликанты.
2 набора называются соседними, если их кодовое расстояние равно 1.
x1x2x3
- > x1x2 - простая импликанта
x1x2x3
100
101
001 = > d = 1
Кодовое расстояние - кол-во единиц в сумме по модулю 2 этих наборов.
100
111
011 => d = 2 - кодовое расстояние.
Минимальное покрытие – минимальное число импликант покрывающих все единичные значения.
8 .Методы минимизации булевых функций.
Метод Квайна
Для получения минимальной формы необходимо в СДНФ произвести все возможные склеивания и поглощения так, что в результате будет получена сокращенная ДНФ (СКДНФ).
Полученная СКДНФ может содержать лишние простые импликанты, которые необходимо выявить на втором этапе минимизации.
Удаление лишних простых импликант осуществляется с помощью импликантной таблицы.
Из импликантной таблицы находим обязательные простые импликанты. Т.е. такие импликанты, которые и только они, покрывают некоторый исходный набор. Далее из числа оставшихся простых импликант выбираются те, которые максимально покрывают непокрытые исходные наборы. Если их несколько, то из них выбирается набор имеющий минимальную длину.
Метод Квайна-Макласски
Множество исходных наборов разбивается на подмножества с одинаковым количеством единиц в каждом. Далее выполняется операция по склеиванию соседних множеств. Далее отсортировываем его по местоположению x. Затем склеиваем наборы внутри каждого класса. В результате получаем сокращенную ДНФ. Для нахождения минимальной ДНФ следует построить импликантную таблицу и выполнить операции с ней по методу Квайна.
Алгоритм Рота
Метод Рота ориентирован на задание переключательных функций в форме произвольного кубического покрытия. За счет этого упрощается процесс подготовки функции для минимизации. Главным достоинством алгоритма является полная формализация действий на всех этапах минимизации.
Минимизиpyющие карты Вейча, Карно.
Минимизиpyющие карты Вейча и Карно являются одним из методов представления булевых функций от небольшого числа переменных.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.