Код 8421 является взаимодополняемым до 15, это создает неудобство при суммировании чисел, приходится вводить поправку. Но имеется одно существенное достоинство, аддитивность, т.е. сумма кодов равна коду суммы.
Суммирование чисел с одинаковыми знаками в коде 8421:
1. (a + b)<= 9. В этом случае никаких поправок вводить не надо.
2. 10<=(a + b) <= 15 В этом случае необходимо ввести поправку.
Наряду с формированием принудительной единицы переноса в старшую тетраду, в текущую тетраду добавляется поправка 0110 (равная 6 десятичной), которая формирует в тетраде результата 16-ричный перенос, уже учтенный схемой (игнорируется).
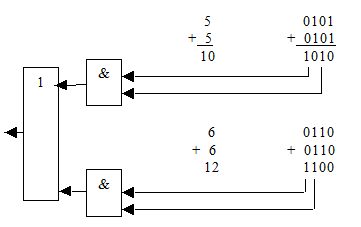
Перегонка “10” осуществляется коррекцией “6”
1010
0110
1 0000
 |
1100
0110
1 0010
Сложение чисел с разными знаками.
1. A-B>0
Сложение чисел с разными знаками осуществляется в обратном коде.
В результате инверсии отрицательного числа в тетраду вносится дополнительные 15 единиц, а в результате переноса тетраду покидают 16 единиц. Следовательно, не хватает единицы. По линии циклического переноса единица переноса знакового разряда добавляется в последний разряд.
В случае A-B<0 В результате инверсии отрицательного числа в тетраду вносится дополнительные 15 единиц, а в результате повторной инверсии тетраду покидают 15 единиц.
В случае работы с количеством тетрад в числе > 1 Используется следующее правило:
Если результат положительный, то если из тетрады нет переноса, то заем в нее (коррекция +10).
Если результат отрицательный, то если из тетрады есть перенос, то заем в нее (коррекция +6).
Одноразрядный двоично-десятичный сумматор
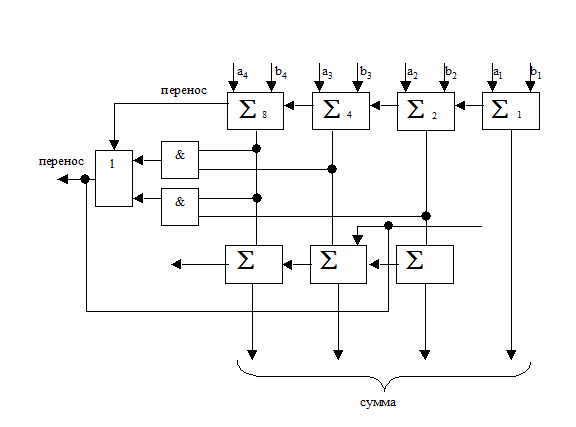
1. Этот код не весомозначный – недостаток.
2. Этот код взаимодополняемый до 9.
Двоично-десятичные коды с избытком три.
Рассмотрим два случая:
1. A+B<=9
Для получения ДДК с избытком три необходимо в каждую тетраду добавить избыточную тройку: A+3+B+3<=15
В этом случае в тетраде накапливаются лишние 6 единиц и т.к. код с избытком 3, то необходимо вычесть тройку.
2. A+B>=10
A+3+b+3>=16
В этом случае в результате переноса из тетрады уходят 16 единиц (10+3 – перенос и 3 – избыток результата). Следовательно, в результат необходимо добавить тройку.
Общее правило для суммирования – вычитания чисел в коде с избытком три:
Если из тетрады есть перенос, то в результат прибавим 3, иначе –отнимем 3.
Пример:
A = 169 0.0100 1001 1100
B = 378 0.0110 1010 1011
- 0011 +0011+0011
1000 0111 1010
5+3 4+3 7+3
Двоично-десятичные коды с избытком шесть.
Код получается добавлением к одному из слагаемых шестерки в каждую тетраду. При суммировании чисел в коде с избытком шесть коррекция может понадобиться только в том случае, когда сумма меньше шестнадцати. В остальных случаях возникает перенос, выносящий из тетрады шесть лишних единиц. Коррекции в данном случае не требуется. Результат получается в обычном коде.
7. Способы представления булевых функций.
Пусть х – некоторая логическая переменная. Используя основные положения алгебры логики нетрудно убедиться в верности следующих правил:
x + 1 = 1 x * x = 0
x * 1 = x x + x = 1
x + 0 = x 1 = 0
x * 0 = 0 0 = 1
x + x = 1
x – позволяет исключать выражения имеющие двойное
отрицание заменяя их исходным выражением.
Законы повторения:
x + x + x + x + x + … + x = x
x * x * x * x * x * … * x = x
Законы де Моргана:
x1x2 = x1 + x2
x1 + x2 = x1x2
и следствия из них:
x1x2 = x1 + x2
x1 + x2 = x1x2
Законы де Моргана и следствия из них справедливы для любого количества переменных.
Законы поглощения:
x1+x1x2 = x1
x1(x1+x2) = x1
Закон склеивания:
x1x2 + x1x2 =
x1(x2 + x2) = x1
1. Элементарная конъюнкция – это логическое произведение конечного множества переменных взятых с отрицанием или без него.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.