Сопоставление опытных и расчетных распределений радиальной скорости в пределах ядра потока. Сопоставление расчетных и опытных значений коэффициента крутки для циклонных камер с различной геометрией и степенью загрузки рабочего объема, страница 7

Здесь Y_w – поправочная функция, определяемая по зависимости:

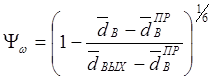,                                    (4.51)

 – значение  при .

На рис.4.27 расчетное уравнение (4.51) сопоставлено с опытными данными.

Как отмечалось выше, зависимость коэффициента сопротивления циклонной камеры кольцевого сечения  от  имеет сложный характер.

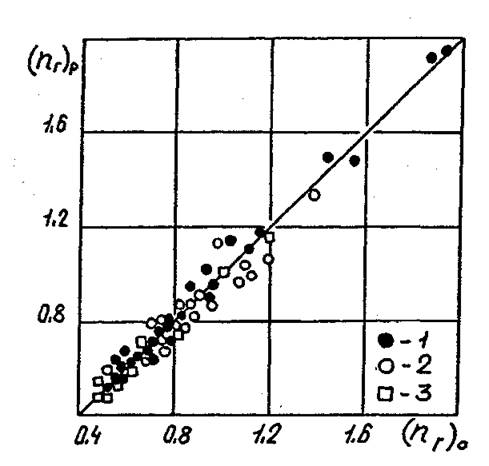
Рис. 4.25. Сопоставление значений показателей аппроксимации (1.8) полученных из опыта  и расчета  в соответствии с формулами (4.46)…(4.48). 1 – опытные данные, полученные в работе; 2 – [63] ; 3 – [51…54].

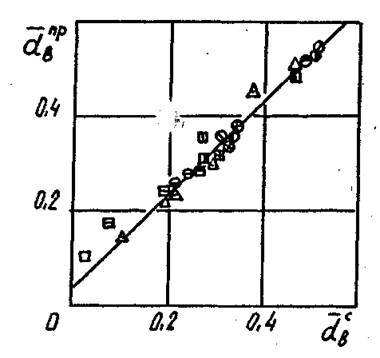
Рис. 4.26. Взаимосвязь значений диаметров вставок  и . Обозначения геометрических характеристик циклонных камер приведены в табл. 4.2.

Если рассматривать изменение  относительно его значения для незагруженной камеры , то с увеличением  первоначально происходит его увеличение, а затем уменьшение и при  . Дальнейшее увеличение  приводит к неограниченному росту  за счет его выходной составляющей. Такое изменение коэффициента сопротивления обусловлено ликвидацией вставкой характерных зон потока (осевого обратного тока, отрицательного давления и т.д.). Нами установлено, что при  максимальное значение коэффициента сопротивления наблюдается при , а минимальное при . В исследованном диапазоне изменения геометрических характеристик циклонных камер кольцевого сечения изменение  по отношению  составляло не более 15%. Поэтому в диапазоне изменения . Для определения  можно воспользоваться одной из методик, существующих для определения  [121], и считать  не зависящим от . При  влияние изменения действительной выходной площади потока на  может быть учтено тем же способом, что и использовался для . В этом случае расчетная формула для коэффициента сопротивления примет вид (рис.4.28):

,                                           (4.52)

где     Y_x – поправочная функция, определяемая по зависимости:

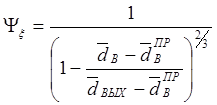.                                   (4.53)

Предложенный метод определения w_jm и  при  нашел удачное применение и для циклонных камер со вставкой некруглого сечения и соответствующим ей по форме выходным отверстием [119].

В общем случае показатели n_w и n_Г не равны между собой определяются по соответствующим зонам согласно уравнений (4.41)…(4.48), (4.36) и (1.11), связывающим между собой n_w, b, h_wm и n_Г, b, h_Гm. Однако указанные уравнения представлены относительно h_wm и h_Гm в неявной форме. Поэтому для нахождения h_wm или h_Гm  (в практическом диапазоне их изменения) с достаточной для технических расчетов точностью могут быть рекомендованы формулы, полученные в результате приближенного решения уравнений (4.36), (1.11).

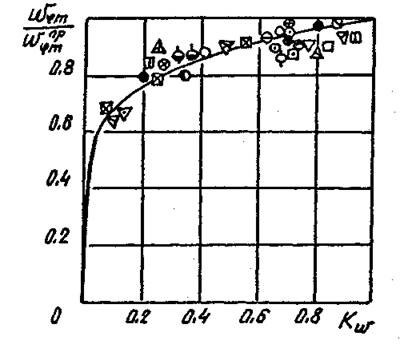
Рис. 4.27. Сопоставление расчетного уравнения (4.50) с опытными данными. Обозначения приведены в табл. 4.2.

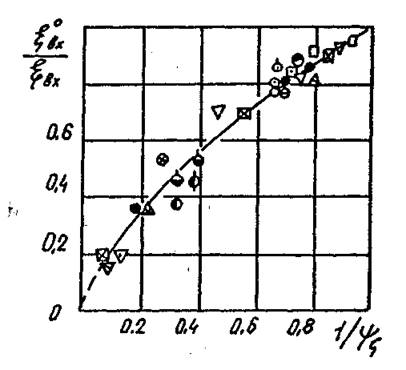
Рис. 4.28. Обобщение опытных данных по коэффициенту сопротивления циклонной камеры кольцевого сечения при . Обозначения приведены в табл. 4.2.

При

,                                        (4.54)

где     .

При

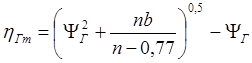,                             (4.55)

где     .

Отметим, что для незагруженных камер (b=0) зависимость (4.36) упрощается

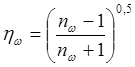,                                       (4.56)

и при  характерные радиусы границ зон связаны соотношением:

,                                            (4.57)

Таким образом используя фрагменты методики аэродинамического расчета циклонных загруженных камер, приведенной в работе [113] и вышеизложенных рекомендациях, можно по заданным их геометрическим параметрам рассчитать распределение скоростей и давлений в рабочем объеме и определить их основные интегральные аэродинамические характеристики. Представленные выше сопоставления показывают, что рассмотренная схема расчета аэродинамических характеристик циклонных камер кольцевого сечения обеспечивает вполне приемлемую для технических расчетов точность,