Сопоставление опытных и расчетных распределений радиальной скорости в пределах ядра потока. Сопоставление расчетных и опытных значений коэффициента крутки для циклонных камер с различной геометрией и степенью загрузки рабочего объема, страница 5

На рис.4.21 проиллюстрирована для одних и тех же условий взаимосвязь экспериментально найденных радиусов вставок , при которых наблюдаются соответственно наибольшие значения  у зависимостей  и наименьшее значение функции . На рис.4.22 показана взаимосвязь расчетных значений  и полученных для аналогичных по геометрии камер опытных значений  при анализе зависимостей  (используемый в уравнении (4.29) показатель n_w определялся по профилю w при b=0).

Анализ полученных в диссертационной работе данных показал, что схема аэродинамического расчета [113,121] может быть использована для циклонных кольцевых камер, но нуждается в усовершенствовании за счет уменьшения погрешности определения отдельных характеристик, а также за счет упрощения (без снижения точности) некоторых связей и зависимостей. Это особенно важно с точки зрения повышения расчетной точности приведенных далее обобщенных уравнений конвективного теплообмена. Следует также ввести дополнительные ограничения и поправочные соотношения для вариантов камер с таким сочетанием параметров  и , при которых внутренняя цилиндрическая вставка, проходящая через выходное отверстие, уменьшает действительную площадь выхода газов. (Последнее приводит к резкому увеличению выходной составляющей суммарного коэффициента сопротивления камеры, его общему уровню и снижению относительной максимальной тангенциальной скорости потока по сравнению со значениями указанных характеристик в вертикальных циклонных загруженных камерах тех же геометрических параметров). Целесообразно для циклонных камер кольцевого сечения принять ранее разработанную схему определения  [113], т.к. она соответствует физической картине движения потока в рабочем объеме, наблюдаемой в зависимости от положения максимума w_j относительно поверхности вставки. В связи с этим в работе выполнено уточнение эмпирических уравнений, входящих в схему определения положения  для рассматриваемой конструкции камер.

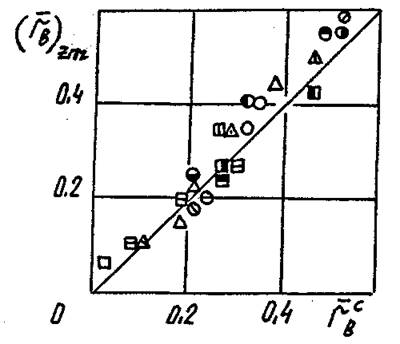
Рис. 4.21. Взаимосвязь экспериментально найденных радиусов вставок  и  соответствующих наибольшему значению w_zm и максимальному значению функции . Обозначения приведены в табл. 4.2.

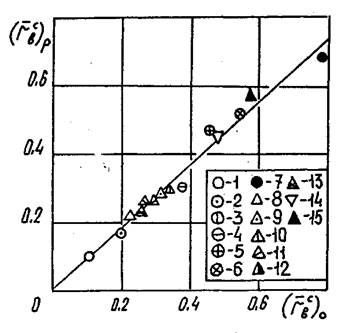
Рис. 4.22. Взаимосвязь значений радиусов вставок  и  ( при b=0). D_k=0,31 м, =0,58 м, = 9,36: 1 – = 0,2; 2 – 0,3; 3 – 0,4; 4 – 0,5; 5 – 0,6; 6 – 0,7; 7 – 1,0. D_k=0,201 м: 8 – =6,3; =0,3; 9 – 6,3; 0,4; 10 – 4,0; 0,4; 11 – 0,2; 0,4; 12 – 6,3; 0,4; 13 – 10,1; 0,4; 14 – 6,3; 0,6; 15 – 6,3; 0,7 [51…54, 63].

В циклонной камере кольцевого сечения безразмерный радиус может быть определен и по эмпирической формуле:

.                                    (4.41)

(При подборе эмпирических формул, приведенных в рассматриваемом разделе работы, кроме результатов наших исследований были использованы экспериментальные данные, полученные в работах [51,52,53,54].)

Каждому характерному диаметру  соответствует определенное расстояние на котором удален максимум w_j от поверхности вставки . Величина этого удаления зависит не только от условий ввода и стока потока, но и шероховатости поверхности стенок камеры:

,                           (4.42)

где      – относительная шероховатость боковой поверхности камеры.

Если исходное значение , т.е. максимум w_j «прижат» к поверхности, заготовки, величина  может быть найдена непосредственно из данного уравнения, т.е. . Если  (максимум w_j «свободен»), то предварительно определяется величина , а затем уже находится радиус положения максимума тангенциальной скорости по следующему эмпирическому уравнению:

.                         (4.43)

Эмпирические формулы (4.41)…(4.43) могут быть рекомендованы для расчетов в следующих диапазонах основных геометрических характеристик циклонных камер кольцевого поперечного сечения: ; ; ; .