Сопоставление опытных и расчетных распределений радиальной скорости в пределах ядра потока. Сопоставление расчетных и опытных значений коэффициента крутки для циклонных камер с различной геометрией и степенью загрузки рабочего объема, страница 6

Для расчета n_w необходимо предварительное определение b и h_w. При заданном  первоначально по геометрическим и режимным характеристикам необходимо найти . В этом случае значение параметра b будет определено и для нахождения  потребуется дополнительно найти лишь величину .

На рис.4.23 приведены одновременно полученные в опытах (при одинаковых условиях) значения  и . Представленные данные показывают, что между  и  в циклонных камерах кольцевого сечения существует однозначная связь, которая может быть описана уравнением:

                                  (4.44)

или

.                                    (4.45)

Таким образом уравнения (4.41) и (4.44) позволяют определить n_w.

На рис.4.24 представлены сопоставления расчетных (по выше рассмотренным соотношениям) профилей w с опытными. Из рисунка следует, что расчетные распределения w хорошо описывают действительные опытные распределения этой характеристики во внутренней (квазитвердой) зоне ядра потока. Это позволяет рекомендовать предложенную схему расчета для практического использования. Найденное значение n_w дает возможность в первом приближении описать распределения w и во внешней (rвазипотенциальной) зоне. Однако, как отмечалось выше, для точной аппроксимации опытных распределений тангенциальной скорости целесообразно для внешней зоны использовать показатель n_Г. Для его определения при известном параметре b необходимо найти h_Гm. Установленные в работе особенности изменения функции  позволяют усовершенствовать, за счет сокращения числа эмпирических уравнений, схему определения n_Г, предложенную в работе [113]. С этой целью, используя зависимости (4.41) и (4.42), определяем  и , а затем значение параметра b^C по формуле:

.                                          (4.46)

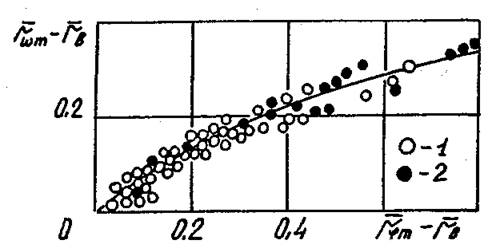
Рис. 4.23. Обобщение опытных данных по  и  в виде зависимости (4.44) для циклонных камер кольцевого сечения. 1 – опытные данные, полученные в работе; 2 – [63].

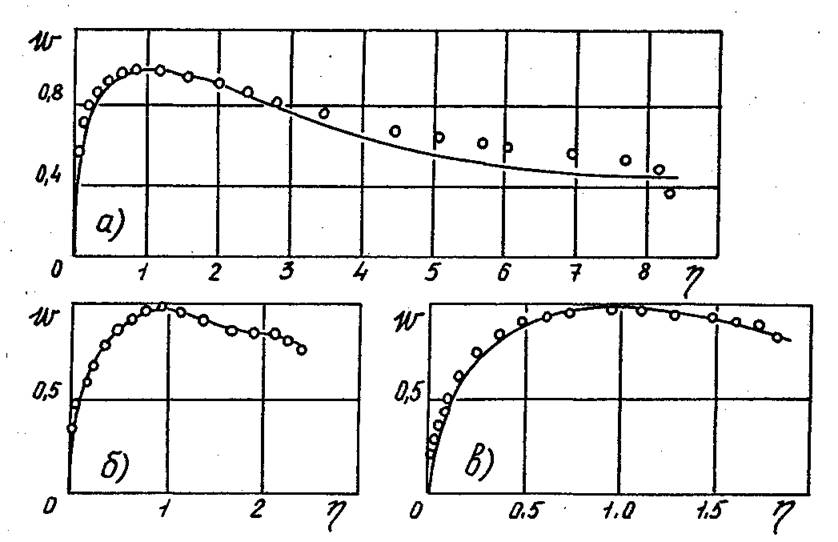
Рис. 4.24. Сопоставление расчетных распределений w с опытными данными при различных значениях параметра b. а – b=4,65 (;); б – b=1,29 (;); в – b=0,49 (;).

Безразмерная координата границы ядра потока для рассматриваемых условий

.                                          (4.47)

находится по уравнению (4.40) или табл.4.1 из условия экстремума функции . Далее из формулы (4.47) определяем

.                                (4.48)

Полагая, что внешняя граница ядра потока не зависит от диаметра внутреннего цилиндра т.е.  [113], находим значение показателя n_Г по формуле (1.11) для заданного найденного по условию задачи параметра b.

Из рис.4.25 видно, что значения показателей аппроксимации (1.8), полученные из опыта  и в соответствии с формулами (4.46)…(4.48)  хорошо согласуются между собой.

В связи с тем, что в рассматриваемых циклонных камерах внутренняя вставка воздействует на движение потока не только в рабочем объеме (как это было при  [113]), но и в выходном отверстии влияние  на  и  при  близких по значениям параметру  оказывается весьма значительным. Как уже отмечалось в гл.1 диаметр вставки, начиная с которого появляются указанные особенности, получил название «предельного»  [114]. Для его определения может быть использована следующая эмпирическая взаимосвязь:

.                                                (4.49)

Зависимость (4.49) сопоставлена с опытными данными на рис.4.26.

Для определения максимальной тангенциальной скорости потока может быть использован метод, предложенный в работах [63,113] (см. формулы (1.12)…(1.14). При , когда вставка уменьшает действительную площадь выходного потока (эта площадь условно нами определяется как разность площади выходного отверстия и поперечного сечения вставки с  для данной геометрии циклонной камеры [119])

,                                         (4.50)