Сопоставление опытных и расчетных распределений радиальной скорости в пределах ядра потока. Сопоставление расчетных и опытных значений коэффициента крутки для циклонных камер с различной геометрией и степенью загрузки рабочего объема

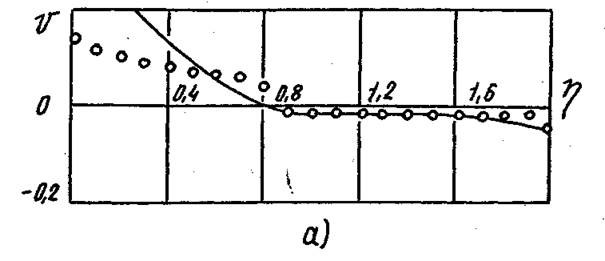
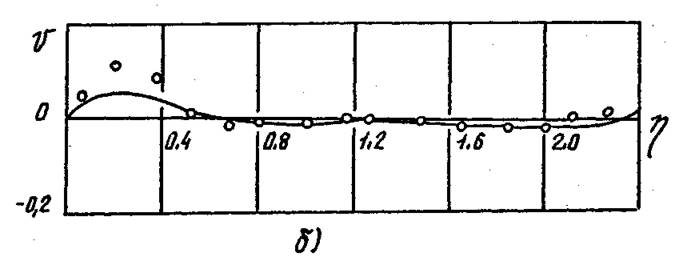
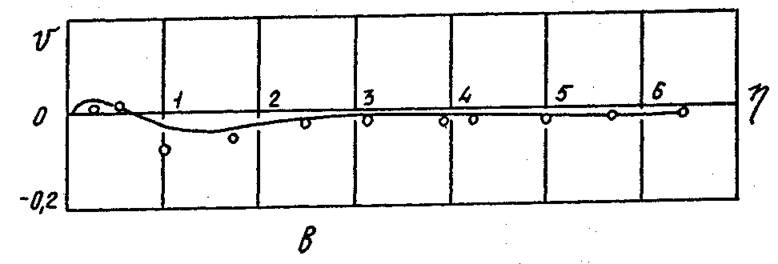
Рис. 4.9. Сопоставление опытных [63] и расчетных распределений радиальной скорости в пределах ядра потока. а – n=1,38, b=0; б – n=0,95, b=0,43; в – n=0,19, b=5,0.

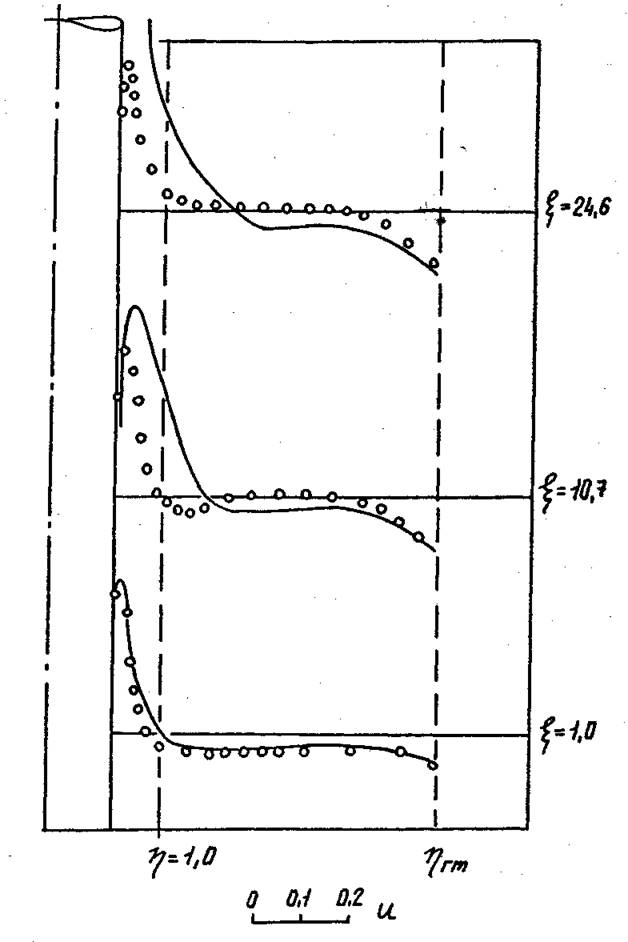
Рис. 4.10. Сопоставление опытных и расчетных распределений u в пределах ядра потока циклонной камеры кольцевого сечения (D_k=0,31 м; ; ; ; n=0,21; b=4,65).

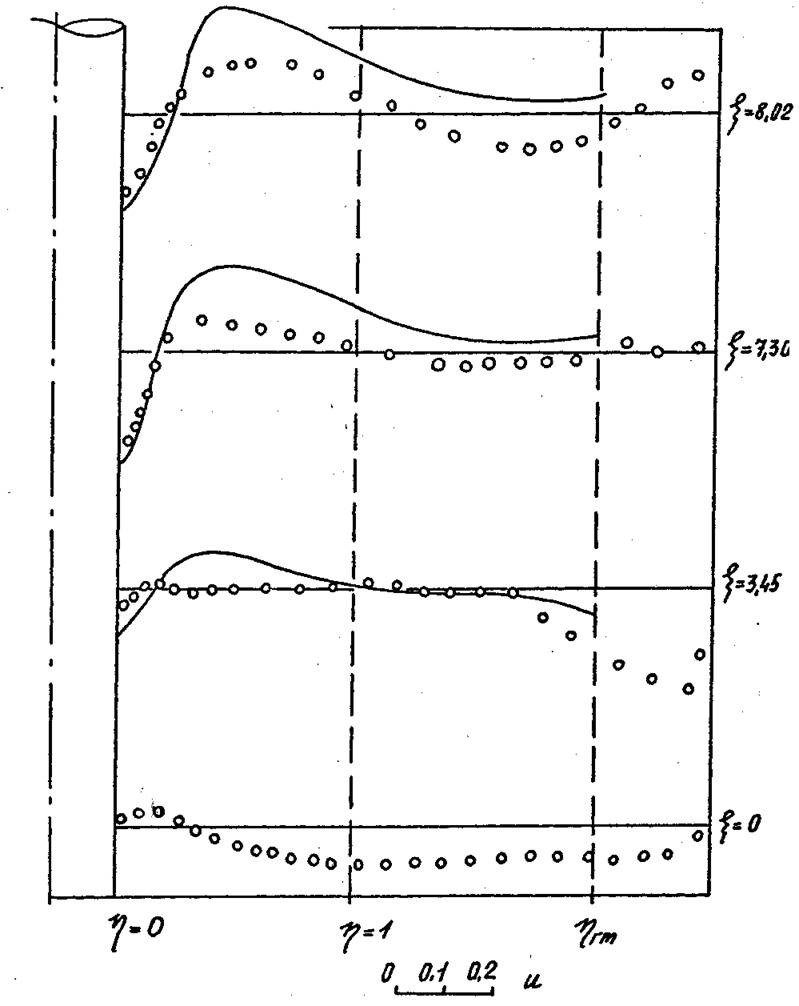
Рис. 4.11. Сопоставление опытных и расчетных распределений u в пределах ядра потока циклонной камеры кольцевого сечения (D_k=0,31 м; ; ; ; n=0,56; b=1,29).

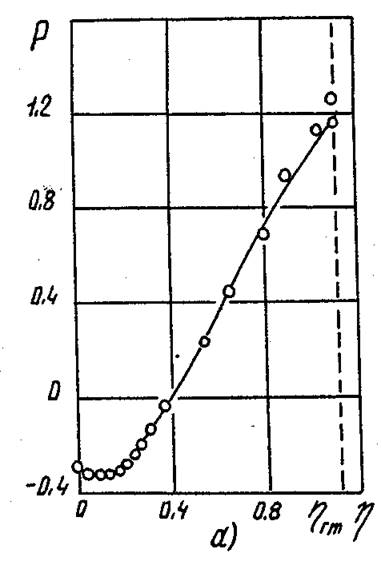
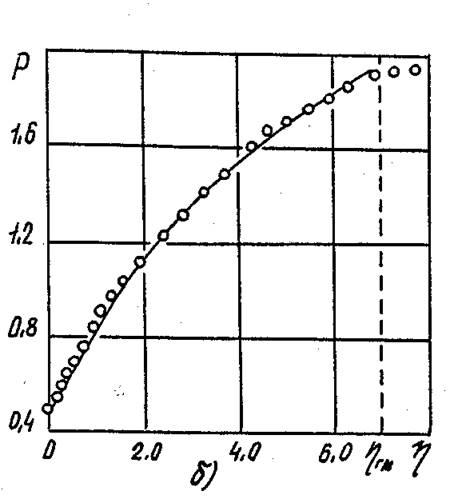
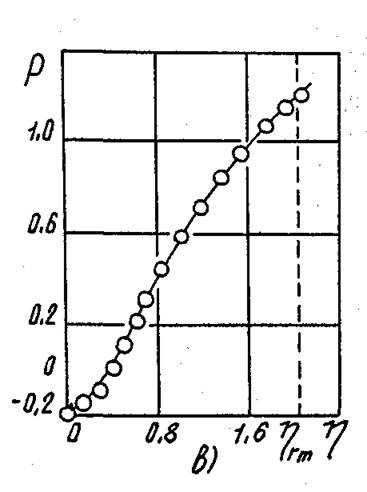
Рис. 4.12. Сопоставление опытных и расчетных распределений Р в пределах ядра потока сечения (D_k=0,31 м; ). а – n=0,8, b=0,28; б – n=0,21, b=4,65; в – n=0,56, b=1,29.

показатель n находили по условиям квазипотенциальной зоны течения. Поэтому в квазитвердой (внутренней) части ядра потока удовлетворительное совпадение расчетных и опытных распределений наблюдается лишь в частных случаях. На рис.4.13 приведено соотношение показателей n_Г и n_О аппроксимации  для квазитвердой зоны, найденных при различной геометрии циклонных камер кольцевого поперечного сечения. (Индекс «Г» показывает, что показатель n_Г определяется по условию максимума циркуляции тангенциальной скорости, т.е. по условиям квазипотенциальной зоны; индекс «О» – по опытным распределениям скорости во внутренней зоне ядра потока.) Из рисунка следует, что погрешность в определении значений n наиболее существенна в распределениях тангенциальной скорости, когда максимум w_j располагается у границы ядра потока или вблизи поверхности вставки.

На рис.4.14 сопоставлены экспериментальные и расчетные данные по распределениям w  во внутренней зоне ядра потока в двух указанных предельных и промежуточном вариантах. Представленные данные подтверждают сделанные выводы. Поэтому, как уже отмечалось, для определения коэффициента a² (распределений u, v, Р), а также ряда других характеристик закрученного потока   (см.гл.4.3), связанных с процессами конвективного теплообмена на поверхности внутреннего цилиндра, более целесообразно находить показатель n аппроксимации (1.8) по условиям внутренней зоны ядра потока. Необходимо отметить, что точность определения взаимных связей у аэродинамических характеристик и тепловых во многом зависит от соответствия действительного и расчетного распределений w именно в указанной зоне течения.

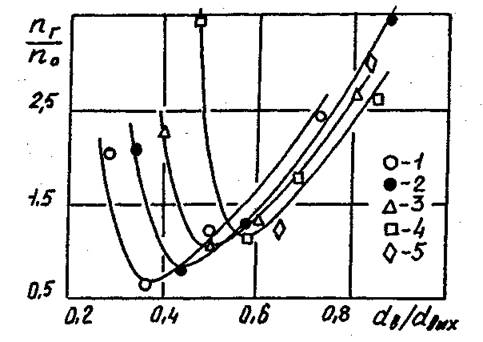
Рис. 4.13. Соотношение показателей аппроксимации (1.8), определенных по методике [63] (n_Г) и опытным путем  (n_О) при различных геометрических параметрах циклонной камеры кольцевого поперечного сечения. 1 –  ; –  ; 3 –  ; 4 –  ; –  .

Для дальнейшего анализа на рис.4.15 представлены распределения безразмерной угловой скорости:

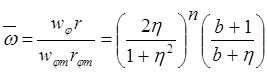,                                    (4.33)

при различных значениях b и n. Учитывая характер распределения  показатель n аппроксимации (1.8) для квазитвердой (внутренней) зоны циклонных камер кольцевого сечения можно определить аналитическим путем.

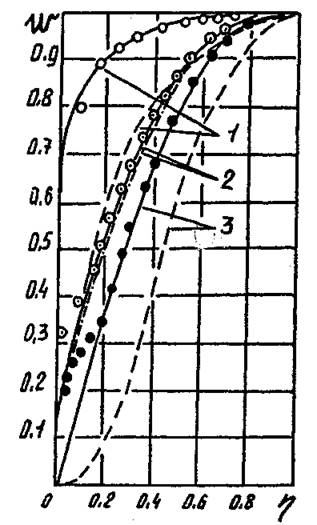
Рис. 4.14. Сопоставление расчетных распределений  с опытными данными. 1 – ; 2 – ; 3 –  (D_k=0,31 м; ). Штриховые линии – расчет по методике [63], сплошные линии – с использованием формулы (4.36).

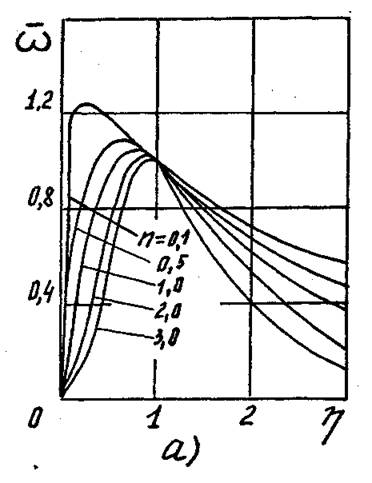
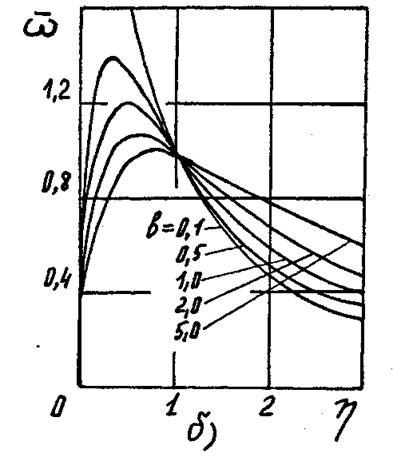
Рис. 4.15. Распределения  в пределах ядра потока циклонной камеры кольцевого сечения при различных значениях параметров n и b.  а – b=2,0; б – n=0,5.

С этой целью в качестве условия для нахождения внешней границы внутренней зоны примем условие максимума угловой скорости вращения потока:

.                                                (4.34)

Используя ранее введенную безразмерную координату h и приняв за масштаб скорости значение w_jm, уравнение (4.53) приводим к безразмерному виду:

.                                              (4.35)

Отсюда при принятой аппроксимации (1.8) показатель n с безразмерной внешней границей внутренней зоны ядра вращающегося потока h_wm будет связана соотношением:

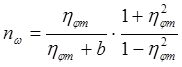.                                        (4.36)

Индекс «w» показывает, что показатель n_w определен из условия максимума угловой скорости вращающегося потока, т.е. по условиям его внутренней зоны.

Внутренняя вставка в циклонной камере кольцевого сечения играет роль аэродинамического стабилизатора. Это приводит к существенному уменьшению зависимости распределения тангенциальной скорости от продольной координаты по сравнению с обычной (незагруженной) камерой. Поэтому при анализе рассматриваемой задачи (как и в работе [113]) принято, что в данной зоне распределение w определяется только значениями показателя n и текущего радиуса.