Промышленность \ Промышленные тепломассообменные процессы и установки

Конструирование сальникового подогревателя типа ПС-115 улучшенных характеристик, страница 3

No=1,0531,163xrw3,                                      (III.5)

где 

x – коэффициент трения движения;

r – плотность греющего теплоносителя при средней температуре, кг/м3.

w – cкорость нагреваемого теплоносителя (воды);

No1=1,0531,163x1rw13 =1,0531,1630,02602998,213=31,81 Вт/м2

No2=1,0531,163x2rw23 =1,0531,1630,02188998,223=213,96 Вт/м2

 

    Также найдем логарифмы:

*( No1) =31,81 =1,5

      ( No2) =213,96 = 2,33

Теперь для определения энергетически оптимальной поверхности необходимо полученные данные для двух точек свести в таблицу 1.

Таблица 1.    Сводная по гладкой трубе.

w1=1 м/с – cкорость нагреваемого теплоносителя для первой точки (воды);

w2=2 м/с – cкорость нагреваемого теплоносителя  для второй точки (воды);

;

;

Nu1 = 170,25;

Nu2 = 269,85;

 Вт/(м2К);

 Вт/(м2К);

;

;

;

;

            No1=31,81 Вт/м2;

                 No2=213,96 Вт/м2;

.

.

2.  Труба с ленточными завихрителями. Эскиз трубы с поперечной накаткой представлен на рис.3.

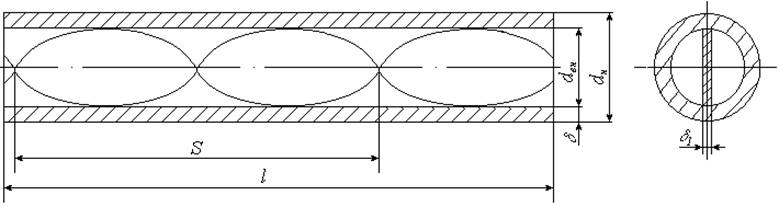
Рис.3. Труба с ленточными завихрителями.

Примем конструктивно , скорость оставим такую же.

ё) Определим эквивалентный диаметр:

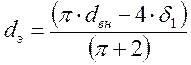                                    ,                                     (III.6)

где

dвн= dн-2dмм – внутренний диаметр  стальных трубок, dвн=25–3=22 мм ;

dэ – эквивалентный диаметр ;

d1=1мм – толщина ленты;

p - число Пи p=3,14;

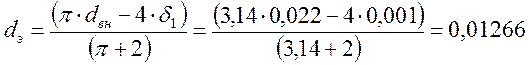м.

ж) Рассчитаем диаметр кривизны.

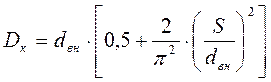                                ,                                   (III.7)

где

Dк – диаметр кривизны;

S – полный шаг закрутки потока;

dвн– внутренний диаметр трубы, м;

p - число Пи p=3,14;

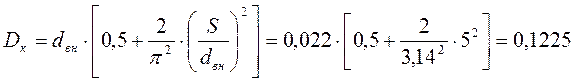м.

з) Определим критические числа Рейнольдса:

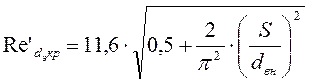                                ,                             (III.8)

где

S – полный шаг закрутки потока;

dвн– внутренний диаметр трубы, м;

p - число Пи p=3,14;

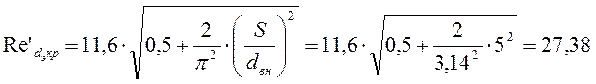
Найдем второе число Рейнольдца.

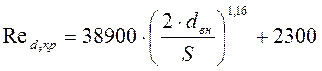                                                         (III.9)

Преобразуем формулу (III.9)

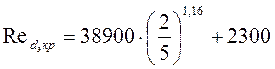
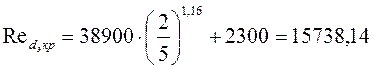
Также по формуле представленной ниже найдем

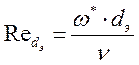                                                       ,                                  (III.10)

где

w*– скорость нагреваемого теплоносителя, м/с;

dэ– эквивалентный диаметр трубы, м;

n – кинематическая вязкость, м2/с.

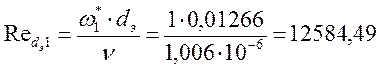
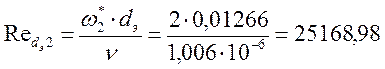
и) Коэффициент трения движения:

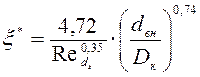                                ,                                             (III.11)

где 

x*– коэффициент трения движения

dвн– внутренний диаметр трубы, м;

 – число Рейнольдса;

Dк – диаметр кривизны;

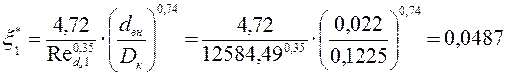
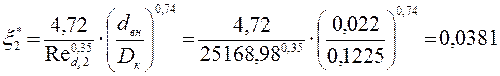
й) Найдем число Нуссельта для первого так как оно удовлетворяет  условию :

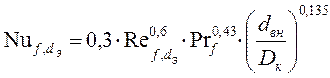                           ,                           (III.12.а)

где

– число Рейнольдса;

Prf – число Прандтля;

Dк – диаметр кривизны.

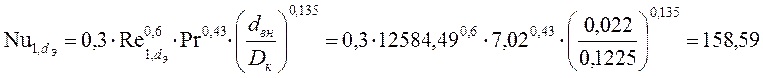
й’) Найдем число Нуссельта для второго так как оно удовлетворяет  условию :

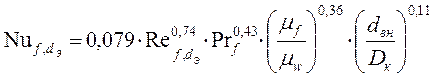                          ,             (III.12.б)

где

m f = 100410-6 Нсек/м2 – коэффициент динамической вязкости при средней температуре воды;

m w = 549,410-6 Нсек/м2 – коэффициент динамической вязкости при средней   температуре стенки;

– число Рейнольдса;

Prf – число Прандтля;

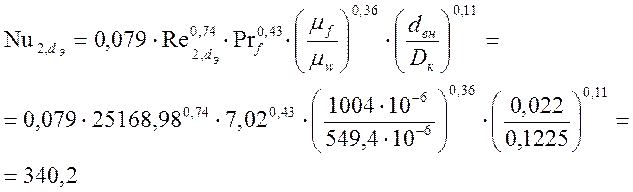
к) Определим коэффициент теплопередачи:

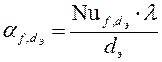                                       ,(III.13)

где

Nu– число Нуссельта;

l = 59,910-2 Вт/мград – коэффициент теплопроводности; 

dэ– эквивалентный диаметр трубы, м;

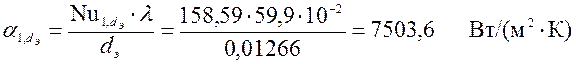
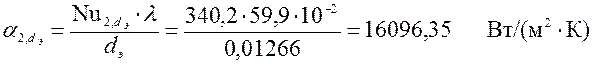
Найдем логарифмы:

*(a1) =7503,6 = 3,875

                                       *(a2) =16096,35 = 4,208

л) Потребляемая мощность, Вт/м2:

No,d = 1,0531,163x *r(w *)3,                                      (III.14)

где 

x* – коэффициент трения движения;

r – плотность греющего теплоносителя при средней температуре, кг/м3.

Скачать файл