Конструирование сальникового подогревателя типа ПС-115 улучшенных характеристик, страница 2

где

F – площадь поверхности теплообмена;   

Dt_ср – средний температурный напор аппарата,°C;

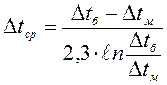                                               ,                                         (II.4.а)

где

                  Dt_б – большая разность температур теплоносителей,°C;

                  Dt_м – меньшая разность температур теплоносителей,°C;

K – коэффициент теплопередачи, Вт/м²К

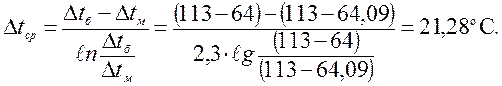
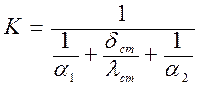                                                       (II.4.б)

где

a₁ – коэффициент теплоотдачи греющего теплоносителя;

a₂– коэффициент теплоотдачи нагреваемого теплоносителя;

d_ст– толщина стенки трубки, м;

l_ст – коэффициент теплопроводности стенки, Вт/(мК).

Расчет коэффициента теплопередачи представлен в тепловом расчете аппарата. Он берется для стали  12Х18Н10Т равным  l_ст= 15,98 Вт/(мК) по справочнику [3].

 III. Выбор оптимальной поверхности теплообмена по энергетическим характеристикам.

Сравним поверхность теплообмена между гладкими трубами и трубами с ленточными завихрителями и выберем наиболее эффективные. В конце расчета (сравнения) будет построен график эффективности . Поэтому в расчете для построения его будут использоваться две скорости.

1.  Гладкая труба. Эскиз гладкой трубы представлен на рис.2.

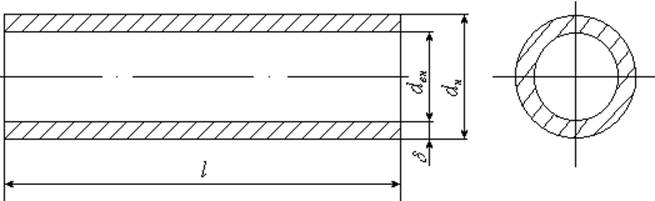
Рис.2. Гладкая труба.

а) Введем предварительно следующие обозначения.

Все представленные ниже параметры взяты при температуре t_cp = 20 ^оС для воды.

l= 65,910^-2 Вт/мград – коэффициент теплопроводности воды; 

n = 0,47810^-6м²/с – кинематическая вязкость воды;

r =980,2 кг/м³ – плотность нагреваемого теплоносителя воды;

Pr = 2,81 – число Прандтля;

d_н=19мм – наружный диаметр  стальных трубок;

d_вн= d_н-2dмм – внутренний диаметр  стальных трубок, d_вн=19–2=17 мм ;

d =1 мм – толщина трубки;

w₁^*= w₁ =1 м/с – cкорость нагреваемого теплоносителя для первой точки     

(воды);

w₂^*=w₂ = 2 м/с – cкорость нагреваемого теплоносителя  для второй точки  

(воды);

б) Определяем число Рейнольдса:

                                  ,                                               (III.1)

где

w– скорость нагреваемого теплоносителя, м/с;

d_вн– внутренний диаметр трубы, м;

n – кинематическая вязкость, м²/с.

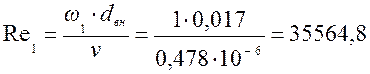
в) Найдем число Нуссельта:

Для определения теплоотдачи в турбулентном режиме движения жидкости внутри прямых гладких труб и каналов большой длины рекомендуется использовать полуэмпирическое соотношение Михеева, для нахождения Nu :

                        ,                         (III.2)

где

Re – число Рейнольдса;

Pr – число Прандтля;

Pr_cт – число Прандтля для стенки

Число Прандтля Pr принимаем по средней температуре:

                                            t_cp=0,5(t₂’+ t₂”),                                (III.2.1)

где  

t₂’ = 15^оС – температура нагреваемого теплоносителя на входе;

t₂” = 25 ^оС – температура нагреваемого теплоносителя на выходе.

t_cp = 0,5(64+64,09)=64,045 ^оС.

По [5] находим значение числа Прандтля для воды : Pr=2,81.

Также находим Прандтль Pr_стпринимаем по средней температуре стенки:

t_cт=0,5(t_ср1+ t_ср2),                                 (III.2.2)

где  

t_ср1= 20^оС – средняя температура нагреваемого теплоносителя ;

t_ср2= 80,1^оС – средняя температура греющего теплоносителя .

t_cт = 0,5(64,045+113)=88,5 ^оС.

По [5] находим значение числа Прандтля для стенки : Pr_ст=1,99.

г) Определим коэффициент теплопередачи:

                                                 ,(III.3)

где

Nu – число Нуссельта;

l = 59,910^-2 Вт/мград – коэффициент теплопроводности; 

d_вн= 0,022м внутренний диаметр.

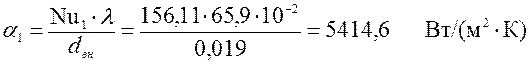
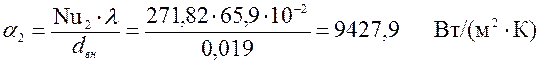
Найдем логарифмы:

(a₁) =5414,6 = 3,73

      (a₂) =9427,9 = 3,97

д) Коэффициент трения движения:

                                          ,                                          (III.4)

где 

x– коэффициент трения движения

Re – число Рейнольдса;

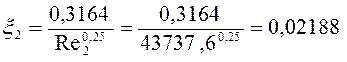
е) Потребляемая мощность, Вт/м²: