Суммирование рядов и последовательностей. Метод суммирования средних арифметических

Лекция 7

Суммирование рядов и последовательностей

Определение 1 (метод Чезаро суммирования средних арифметических)

1) Пусть  последовательность (действительных ил комплексных чисел), . Если $ конечный или равный ±¥ предел  Þ последовательность  суммируется методом средних арифметических к .

2) Пусть  – ряд (действительных или комплексных чисел), . Если последовательность частичных сумм  суммируется методом средних арифметических к s – числу или ±¥, то s – сумма ряда  в смысле среднего арифметического.

Определение 2

1) Метод суммирования – линейный, если из того, что он суммирует последовательность  к числу А следует, что для "a он суммирует последовательность  к числу aА, а из того что он суммирует последовательности  и  к числам А и В следует, что он суммирует последовательность  к числу А+В.

2) Метод – регулярный, если " сходящуюся последовательность он суммирует к ее пределу.

3) Метод – вполне регулярный, если он регулярный и " расходящуюся и ±¥ последовательности суммирует к ±¥ соответственно.

Теорема 2

Метод суммирования средних арифметических (Чезаро) линеен и вполне регулярен.

Доказательство

1*) Пусть  . Если .

2*) Если  .

Пример 1

1) Пусть .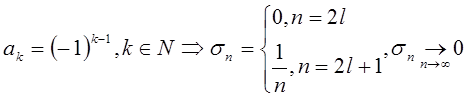

2) Ряд .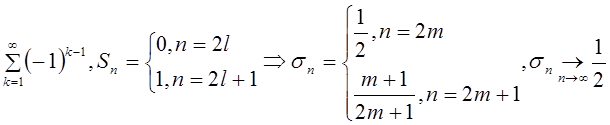

Теорема 3

Если последовательность S_n (ряд ) суммируется методом средних арифметических к некоторому числу Þ S_n=o(n) и a_k=o(n).

Доказательство

.

.

Определение 2 (метод суммирования Абеля) Пусть дан ряд .

1) Если , ряд  сходится и  – число Þ ряд  суммируется методом Абеля к числу s.

2) Если , ряд  сходится или расходится к ±¥ и , то ряд  суммируется методом Абеля к ±¥.

3) Последовательность суммируется методом Абеля к числу или ±¥, если ряд, последовательность частичных сумм которого она является, суммируется методом Абеля.

Теорема 4 (Фробениуса)

Если ряд (последовательность) суммируется методом средних арифметических к числу s Þ он (она) суммируется методом Абеля к s.

Доказательство

 Заметим, что . Ряды  сходятся при |r|<1 по признаку Коши:  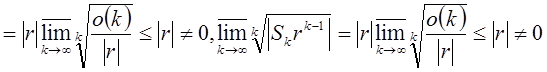. Имеем

. Заметим, что  . Пусть a₁=1, a_k=0 при k>n .

  Þ ряд суммируется мтодом Абеля к S.