Определение главной передаточной функции замкнутой САР

Министерство образования Республики Беларусь

Белорусский Национальный Технический Университет

Кафедра“Гидропневмоавтоматика и гидропневмопривод”

Группа 101714

Расчетная работа №1

по дисциплине “Теория автоматического управления”

Выполнил

Руководитель:                                                            

Расчетная работа №1

Исходные данные

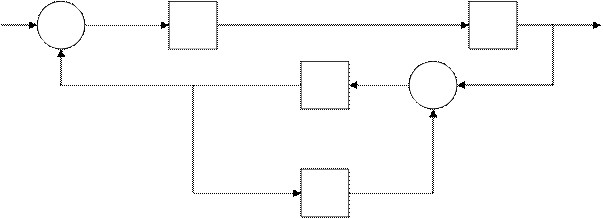
Схема:

Уравнения:

1. 0,7d^2∙y₁/dt² + 4,5dy₁/dt + 1,4y₁ = 20x₁

2. 0,7dy₂/dt + 4,5y₂ = 9,8x₂²

3. 4,5y₃ = 9,8dx₃/dt + 20x₃

4. 1,4y₄ = 2,7x₄

6. 2,7y₆ = 20x₆

h=30; g₀=20; g₁=60; g₂=20; a=0,7; C=1,5; X₀=1,6

1.  Приравнивая к нулю все производные в заданных уравнениях движения звеньев, получаем уравнения статических характеристик последних. На исходной схеме САР необходимо обозначить входные x_i и выходные y_i сигналы каждого звена:

1. 1,4y₁ = 20x₁                y₁ = 14,3x₁

2. 4,5y₂ = 9,8x₂²              y₂ = 2,2x₂²

3. 4,5y₃ = 20x₃                         y₃ = 4,44x₃

4. 1,4y₄ = 2,7x₄                      y₄ = 1,9x₄

6.  2,7y₆ = 20x₆               y₆ = 7,41x₆

Построение результирующей статической характеристики САР выполняется по этапам:

1) строим частичную результирующую характеристику для соединения с параллельной связью звеньев 3 и 6 (рис. 1). Получаем звено 7 (y₇=x_oc1):

 

2) строим частичную результирующую статическую характеристику для соединения с отрицательной связью звеньев 2 и 7 (рис. 2). Получаем звено 8 (y₈=x_oc2):

 

3) строим частичную результирующую статическую характеристику для соединения с последовательной связью звеньев 1 и 4 (рис. 3). Получаем звено 9:

 

4) статическая характеристика САР (рис. 4).

2.  Звено 2 – нелинейное. Нелинейной функцией является f(x₂)=2,18x₂². Линеаризация этой функции производится методом разложения ее в ряд Тейлора с последующим отбрасыванием всех малых членов разложения. Исходный режим линеаризации задан координатой  x₀.

∆y=(dy/dx₂)_x ∆x₂

y=(dy/dx₂)_x x₂

y=(2,18∙2∙x₂)_x x₂=4,36∙1,6∙x₂=6,98x₂

3.  Уравнения движения сначала приводятся к стандартной форме записи, затем записываются в изображениях по Лапласу, и находятся передаточные функции звеньев. Далее определяются основные параметры звеньев: коэффициенты передач K_j; постоянные времени T_j; коэффициент относительного демпфирования ξпервого звена. Затем уравнения движения звеньев необходимо записать в  изображениях по Лапласу через передаточные функции, по которым строим структурную схему САР.

Первое звено:     0,7d^2∙y₁/dt² + 4,5dy₁/dt + 1,4y₁ = 20x₁

Запишем в стандартном виде:   0,5d^2∙y₁/dt² + 3,2dy₁/dt + y₁ = 14,3x₁

Найдем коэффициенты:     Т₁² = 0,5;   Т₁ = 0,71

2ξ₁Т₁ = 3,2;   ξ₁ = 2,25

К₁ = 14,3

Запишем уравнение в изображениях по Лапласу:

d²y₁/dt² = S₁²y₁(S)          dy₁/dt  = S₁y₁(S)

   y₁ = y₁(S)           x₁ = x₁(S)          

(0,5S² + 3,2S + 1)y₁(S) = 14,3x₁(S)

Из предыдущего уравнения найдем передаточную функцию:

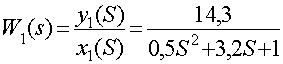
Данное звено является апериодическим второго порядка.  

Второе звено:

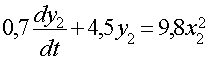
Для того чтобы это уравнение записать в стандартном виде необходимо пролинеаризовать :

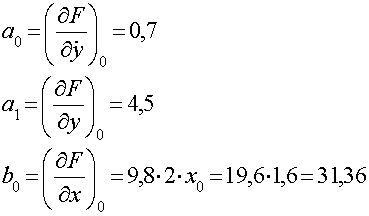
Запишем в стандартном виде:

     

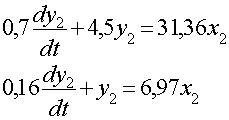
Найдем коэффициенты из предыдущего уравнения:

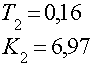
Предыдущее уравнение запишем в изображениях по Лапласу:

                          

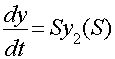
Найдем передаточную функцию:

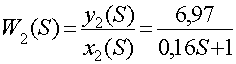
Данное звено является апериодическим первого порядка.

Третье звено:  

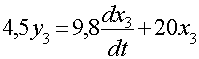
Запишем в стандартном виде:

     

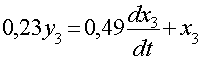
Коэффициенты :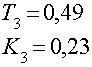           

Запишем уравнение в изображениях по Лапласу:

     

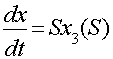
Передаточная функция данного уравнения:

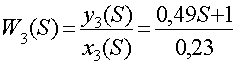
Данное звено – форсирующее первого порядка.

Четвертое звено:

Представим в стандартном виде относительно y:

              

Передаточная функция представляет собой данное отношение:

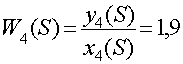
Данное звено является безинерционным.

Шестое звено:

Представим в стандартном виде относительно y:

              

Передаточная функция представляет собой отношение:

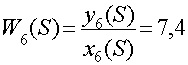
Данное звено является безинерционным.

4.  Переходная  и весовая  функции 1-го звено определяются по выражениям: