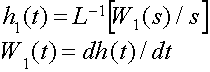
Передаточная функция для первого звена:
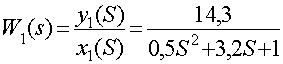
Найдем значение переходной функции:
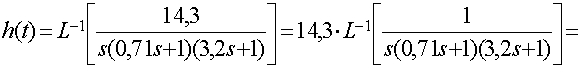
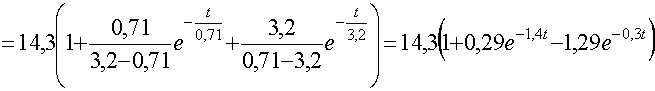
|
t |
0 |
0.25 |
0.5 |
0.75 |
1 |
1.5 |
2 |
3 |
4 |
5 |
|
h(t) |
0 |
0.108 |
0.481 |
1.021 |
1.657 |
3.046 |
4.428 |
6.862 |
8.759 |
10.188 |
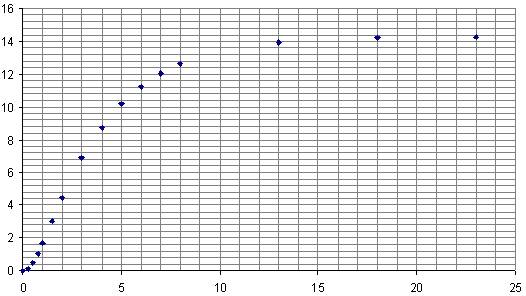
Рисунок 1. Переходная характеристика апериодического звена второго порядка.
Взяв производную от передаточной функции, мы найдем весовую функцию
![]()
|
t |
0 |
0.25 |
0.5 |
0.75 |
1 |
1.5 |
2 |
3 |
4 |
5 |
|
W(t) |
0.28 |
1.493 |
2,255 |
2.704 |
2.941 |
3,027 |
2,852 |
2,279 |
1,729 |
1,291 |
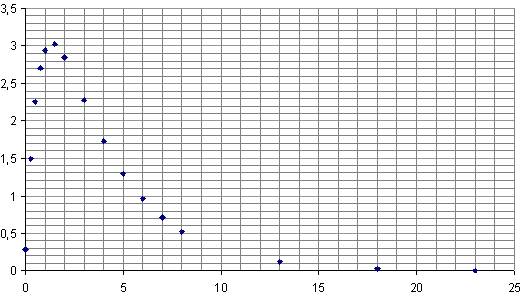
Рисунок 2. Весовая характеристика апериодического звена второго порядка.
5. Найдем выражения для частотных характеристик.
Заменим ![]() и найдем вещественную
и мнимую составляющие передаточной функции
и найдем вещественную
и мнимую составляющие передаточной функции
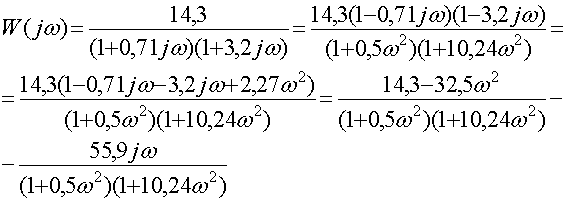
![]()
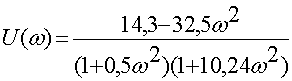
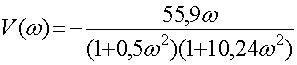
Найдем амплитудно-частотную характеристику (АЧХ)
![]()
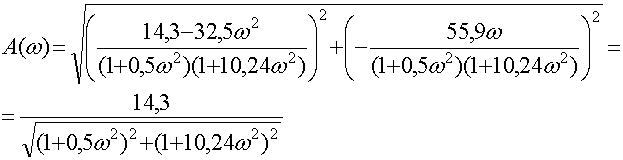
Найдем фазово-частотную характеристику (ФЧХ)
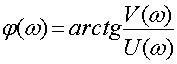
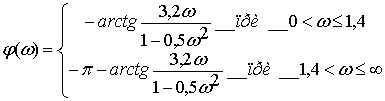
Найдем логарифмическую амплитудно-частотную характеристику (ЛАЧХ)
![]()
Таблица. Результаты расчета частотных характеристик
|
|
0 |
0,11 |
0,53 |
0,71 |
0,96 |
1,29 |
1,73 |
2,28 |
2,85 |
3,03 |
|
|
- |
-1,58 |
-0,93 |
-0,28 |
-0,15 |
-0,02 |
0,111 |
0,238 |
0,358 |
0,455 |
|
|
14,3 |
14,2 |
12,1 |
1,21 |
-0,28 |
-1,03 |
-1,05 |
-0,79 |
-0,59 |
-0,54 |
|
|
0 |
-1,47 |
-5,72 |
-6,73 |
-5,14 |
-3,52 |
-2,18 |
-1,23 |
-0,65 |
-0,37 |
|
|
10,1 |
10 |
9,39 |
3,57 |
2,27 |
1,36 |
0,79 |
0,45 |
0,26 |
0,17 |
|
|
179 |
-174 |
-155 |
-100 |
-87 |
-74 |
-61 |
-49 |
-40 |
-33 |
|
|
20,1 |
20 |
19,5 |
11,1 |
7,11 |
2,67 |
-2,07 |
-6,92 |
-11,6 |
-15,4 |
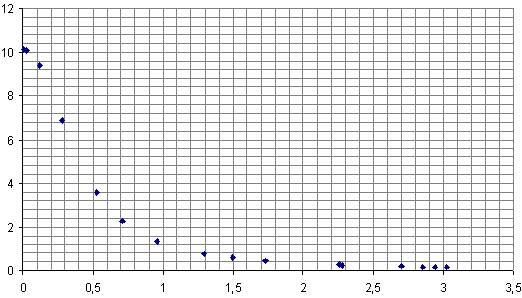
Рисунок. Амплитудно-частотную характеристику (АЧХ)
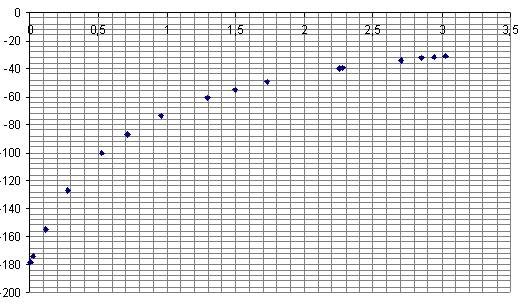
Рисунок. Фазово-частотную характеристику (ФЧХ)
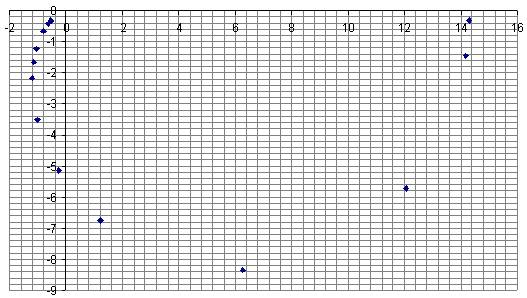
Рисунок. Амплитудно-фазовая частотная характеристика (АФЧХ)
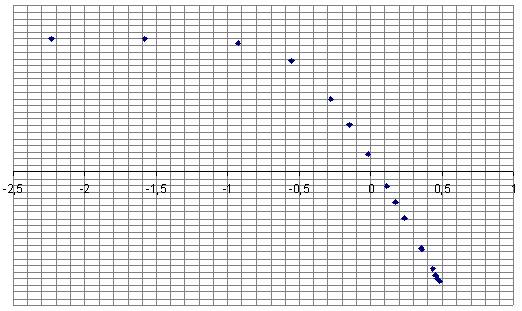
Рисунок. Логарифмическую амплитудно-частотную характеристику (ЛАЧХ)
6. Используя правила преобразования структурных схем, преобразовываем исходную схему в одноконтурную. Определим передаточные функции разомкнутой и замкнутой САР.
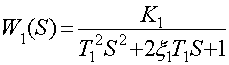
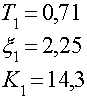
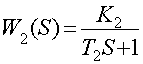
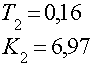
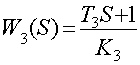
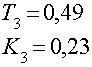
![]()
![]()
![]()
![]()

Рисунок. Исходная структурная схема.
Преобразуем исходную схему в одноконтурную. Для этого заменим местные связи эквивалентными звеньями.
Заменим местную связь с параллельной связью передаточной
функцией ![]() , равной:
, равной:
![]()
Данное звено является безинерционным .
Заменим местную связь с обратной связью передаточной функцией ![]() , равной:
, равной:
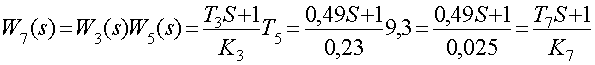
где 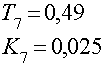
Седьмое звено является – форсирующее первого порядка.

![]()
![]()
Рисунок. Преобразованная структурная схема.
Передаточная функция разомкнутой САР (разомкнута главная обратная связь у узла сравнения)
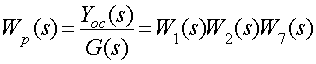
Подставим значения 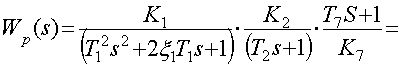
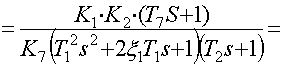
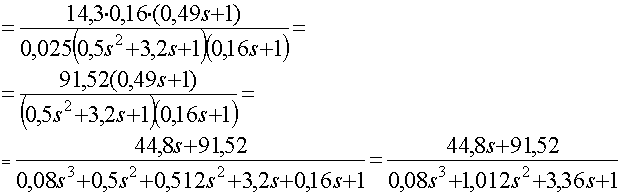
![]()
![]()
![]()
![]()
![]()
Найдем значение ![]()
![]()
![]()
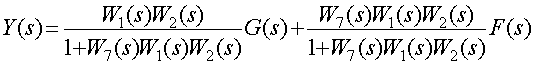
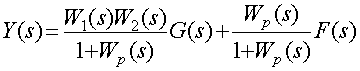
Главная передаточная функция замкнутой САР определяется при ![]()
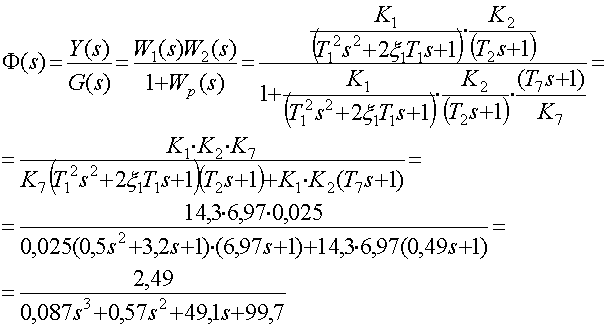
А при ![]() определяется
передаточная функция замкнутой САР по возмущению
определяется
передаточная функция замкнутой САР по возмущению
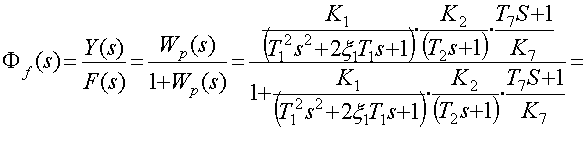
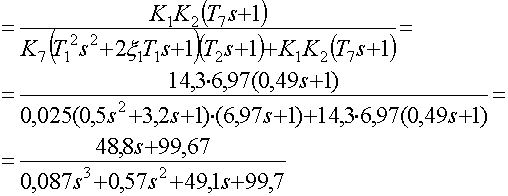
Решим относительно ![]()
![]()
![]()
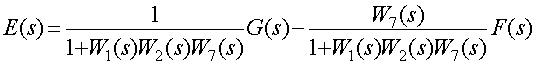
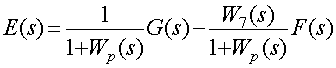
Передаточная функция замкнутой САР для ошибки определяется при
![]()
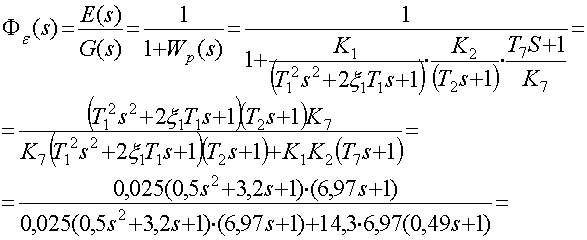
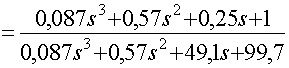
Передаточная функция замкнутой САР для ошибки по возмущению
определяется при условии что ![]()
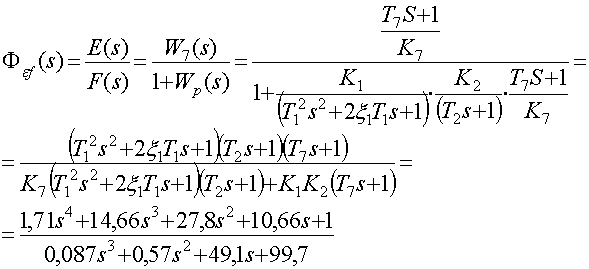
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.