Соотношения между напряжениями и деформациями (Примеры решения задач)

Глава 5

СООТНОШЕНИЯ МЕЖДУ НАПРЯЖЕНИЯМИ И ДЕФОРМАЦИЯМИ

Примеры решения задач

5.1. Показать, что энергия деформации упругого тела, на­ходящегося в напряженном состоянии , не равна сумме энер­гий деформации  и,

т. е.                                              ,

но

                                                    .

Решение. Для вышеуказанных тензоров напряжения мо­жем записать

                           ,

              

                    

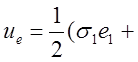
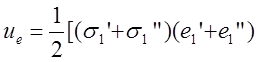
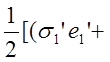
и

                                                 .

      5.2. Стальная деталь нагружена и замерены следующие упругие деформации: , ,  , , . Найти напряженное состояние детали.

Решение. Для вычисления напряжений можно использо­вать уравнение (5.2). Модуль упругости для стали Е = 2,1  10⁴ кГ/мм² и v =0,33. Вычисляем модуль сдвига:

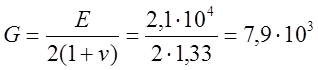                   кГ/мм²

касательные напряжения

                                                  ,

                          кГ/мм²

Нормальные напряжения можно также вычислить, если под­ставить известные деформации в уравнение (5.2), а именно

            ,

          ,

           ,

и решить полученную систему уравнений. Получим следующие напряжения:

             кГ/мм²     кГ/мм²          кГ/мм²

Интересно сравнить среднее напряжение и эффективное на­пряжение с этими напряжениями, а именно,

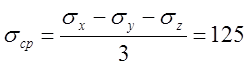                            кГ/мм²

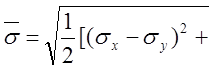
+ кГ/мм²

Следует заметить, что для указанных в этой задаче дефор­маций нормальные напряжения и среднее напряжение очень высокие, в то время как эффективное напряжение остается относительно низким. Если напряжение текучести данного материала выше 30 кГ/мм², как показано в гл. 6, пластическая деформация не начнется, даже если нормальные напряжения будут очень высокими.

5.3. Вычислить главные напряжения и направления для де­формаций в задаче 5.2.

Решение. Эту задачу можно решить с помощью диаграм­мы Мора на рис. 4.3 или с помощью тензора малой деформа­ции в уравнении (4.11), предполагая при этом, что тензор деформации колинеарен тензору напряжения. Фактически эта задача сходна с задачей 4.1, поэтому и решение для направляю­щих косинусов уже имеется. Главные напряжения получаем из определителя

                                     ,

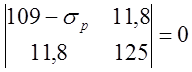который можно привести к квадратному уравнению

                                ,

Получаем два решения

               кГ/мм²икГ/мм²   

Отсюда главные напряжения равны

                                кГ/мм²

                                 кГ/мм²

                                                       кГ/мм²

5.4. При резании автоматной стали энергия пластической деформации концентрируется на очень небольшом участке. Предположим, что эта энергия равна 84 кГм/см³. Вычислить:

а) удельную мощность в киловаттах и б) адиабатическую температуру. Предположим также, что энергия трения равна 1/3 полной энергии, которая требуется для резания.

Решение. Полная энергия резания из условия задачи равна

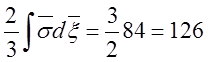                               кГм.

а) Удельную мощность в киловаттах можно вычислить из уравнения (5.19):

Wyg == 126 • 9,81 • 10= 1,23 квт/см³.

б) Адиабатическую   температуру получаем   из уравне­ния (5.21).

Предполагая, что начальная температура равна комнатной,

т е То=20°С, теплоемкость стали в интервале температур 100—200° С    = 0,13 и удельный вес = 0,0078 кГ/см³, имеем

                               .

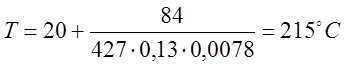Задачи для решения

5 5 Найти общий модуль упругости К и модуль упругости при сдвиге G для трех сплавов — стали, алюминия и магния.

5.6. Вывести следующие зависимости:

а)                            ,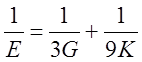

б)                            .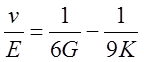

5.7. Пусть тензор упругой деформации записан следующим образом;

                       .                   

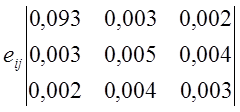Вычислить величину и направление главных напряжений.

5. 8.  Вычислить энергию упругой деформации в задаче 5.7 для случая, когда деформируемым металлом является алюминий.

5.9.Вычислить эффективное напряжение для напряженного состояния, записанного в виде тензора упругой деформации

                              .

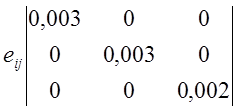5.10. Показать, что член энергии деформации в задаче 5.1 равен нулю, когда —девиатор напряжения и  —сред­нее гидростатическое растяжение.

5.11. Стержень диаметром 25 мм уменьшается в диаметре до 12,5 мм в процессе деформации. Если удельная энергия деформации равна 10³ кГм/см³ и стержень выходит из пресса со скоростью 50 м/ч, вычислить потребную мощность в киловат­тах для пластической деформации (трение не учитывается), а также определить адиабатическую температуру.

5.12. Повторить вычисление задачи 5.11 для пластины тол­щиной 6 мм и шириной 1000 мм, которая выходит из валков прокатного стана с той же самой скоростью и удельной энергией.

1.  В некоторой точке задан тензор напряжений в виде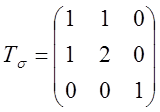

Как следует повернуть систему координат, чтобы тензор имел составляющие находящиеся на главной диагонали?

Круги Мора

1.  Из уравнений кругов мора показать, что точкам на окружностях соответствуют случаи . Указать значения в точках А,В,С,Д,Е,К. Показать что значения находятся в согласии с решением соответствующих уравнений.

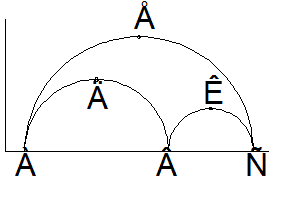Найти графически среднее значение напряжений, если дана конфигурация кругов Мора. Дать доказательство того, что указанная процедура геометрического построения согласуется с алгебраическим уравнением.

2.  Пусть . Вычислить направляющие косинусы в вертикальной точке.

3.  Как найти , если заданы ?

4.  Как из диаграмм Мора показать, что для плоской задачи () можно записать:   

                                     

Семинар 9

Физические уравнения в теории деформаций

1.  Показать аналогию связи между упругими константами и показателями пластического состояния. Указать на различие в определении констант.

2.  Пусть дан тензор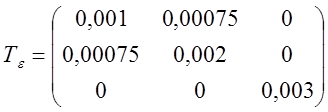

Вычислить главные деформации.

3.  Задан тензор напряжений 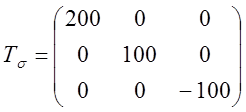. Вычислить величину компонент деформаций если . Вычислить интенсивность деформаций, раскрыть физический и математический смысл этого понятия.