4. Стальная деталь
нагружена и замерены ![]() , модуль пластичности
, модуль пластичности ![]() , среднее нормальное напряжение
, среднее нормальное напряжение ![]() . Записать тензор напряжений и
разложить его на шаровой и тензор-девиатор. Пояснить роль каждого из них в
упруго-пластической деформации.
. Записать тензор напряжений и
разложить его на шаровой и тензор-девиатор. Пояснить роль каждого из них в
упруго-пластической деформации.
5. Задан тензор 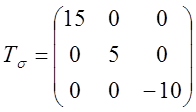 . Записать показатели напряженного
состояния
. Записать показатели напряженного
состояния 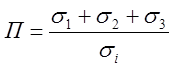 и
и 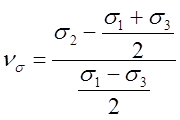 ; и для предельных случаев: плоская
деформация, плоское напряженное состояние, совпадение двух напряжений.
; и для предельных случаев: плоская
деформация, плоское напряженное состояние, совпадение двух напряжений.
6. Показать, что ![]()
3. ТЕОРИЯ ПЛАСТИЧНОСТИ.
Напряжения
в некоторой точке тела равные: ![]() . Может ли металл с
пределом текучести
. Может ли металл с
пределом текучести ![]() МПа (19,6 кГ/мм
МПа (19,6 кГ/мм![]() )
находиться в упругом состоянии?
)
находиться в упругом состоянии?
РЕШЕНИЕ: Используя условие пластичности, получим:
![]()
![]() МПа.
МПа.
![]() МПа.
МПа.
Величина 116258>76832, следовательно, материал не может сохранить упругое состояние.
3.2.
Напряжения в данной точке тела: ![]() , Каким пределом
текучести должен обладать металл, чтобы при заданных напряжениях находиться в
упругом состоянии?
, Каким пределом
текучести должен обладать металл, чтобы при заданных напряжениях находиться в
упругом состоянии?
ОТВЕТ: ![]() МПа.
МПа.
3.3.
Напряжения в данной точке свинцового образца равны ![]() . Напряжение текучести
. Напряжение текучести ![]() МПа.
В каком состоянии находится металл?
МПа.
В каком состоянии находится металл?
3.4.
При испытании на растяжение материала при заданной степени деформации показал ![]() Мпа, (
Мпа, (![]() ).Наложим на схему растяжения шаровой тензор напряжения
).Наложим на схему растяжения шаровой тензор напряжения
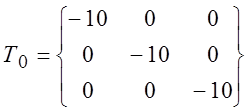 Получим
Получим
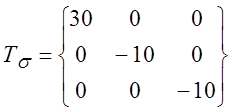
Вычислим из условия пластичности: ![]() ;
1600+0+1600=
;
1600+0+1600=![]()
1600=![]() ;
; ![]() 40
МПа.
40
МПа.
При наложении
шарового тензора ![]() по условию
пластичности не меняется.
по условию
пластичности не меняется.
3.5. Определить
критический размер трещины по Гриффитсу, если модуль нормальной упругости Е=2![]() кГ/мм
кГ/мм![]() ,
удельная поверхностная энергия
,
удельная поверхностная энергия ![]() Дж/см
Дж/см![]() , напряжение в вершине трещины
, напряжение в вершине трещины ![]()
![]() .
.
ОТВЕТ: l=0,2 см.
З.6. Показатели схемы напряженного состояния [7].
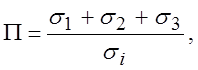
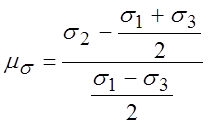 .
.
Их
величины характеризуют схему напряженного состояния и определяют пластичность
материалов при данных условиях деформирования. Вычислить значения показателей ![]() и
и ![]() схемы напряженного состояния для растяжения,
сжатия, кручения и изгибе.
схемы напряженного состояния для растяжения,
сжатия, кручения и изгибе.
3.7. Задан тензор напряжений,
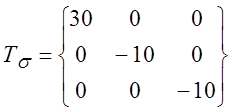
определить
показатели ![]() и
и ![]() .
По величине
.
По величине ![]() к рис. 26 [7] определить величину
критического значения ln для стали У10А.
к рис. 26 [7] определить величину
критического значения ln для стали У10А.
3.8.
Авторы [2] полагают, что пластическое разрыхление можно характеризовать
относительным остаточным увеличением объема ![]() ,
а его приращение
,
а его приращение ![]() пропорционально приращению
степени деформации сдвига:
пропорционально приращению
степени деформации сдвига: ![]() =
=![]() . В момент образования микротрещины
. В момент образования микротрещины ![]() , где
, где ![]() степень
деформации сдвига к моменту разрушения металла - пластичность; она зависит от,
температуры, гидростатического давления (-
степень
деформации сдвига к моменту разрушения металла - пластичность; она зависит от,
температуры, гидростатического давления (-![]() )
интенсивности касательных напряжений
)
интенсивности касательных напряжений ![]() коэффициента
коэффициента ![]() и отношения,
и отношения, ![]() .
.
Определить
пластичность (степень деформации сдвига) стали З0ХГСА с учетом показателя
схемы напряженного состояния и отношения ![]() по
диаграмме пластичности (рис.3.1 [2]), если задан тензор напряжения.
по
диаграмме пластичности (рис.3.1 [2]), если задан тензор напряжения.
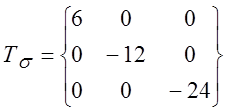
РЕШЕНИЕ:
При испытании на растяжение, 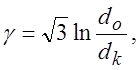
![]() и
и ![]() - диаметры образцов до и после
испытания. При испытании на кручение
- диаметры образцов до и после
испытания. При испытании на кручение ![]() ;
; ![]() - угол наклона образующих линии после испытаний к оси образца.
- угол наклона образующих линии после испытаний к оси образца.
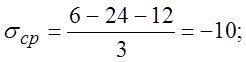
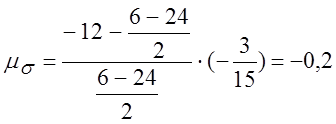 ;
;
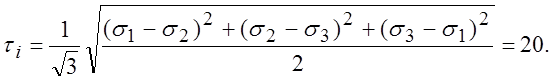
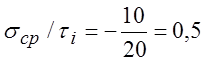 ;
; 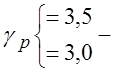 по
диаграмме пластичности;
по
диаграмме пластичности;
![]()
![]() ;
; 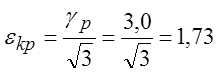 ;
; 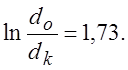
Глава 6
ДЛЯ ИЗОТРОПНОГО УПРОЧЕННОГО МЕТАЛЛА
Примеры решения задач
6.1. Предположим,
что труба, имеющая внутренний радиус ![]() мм и
толщину стенки
мм и
толщину стенки ![]() мм, испытывалась в
условиях двухосного растяжения
мм, испытывалась в
условиях двухосного растяжения 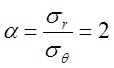 . Найти полное
осевое усилие и компоненты напряжения, если предел текучести материала
. Найти полное
осевое усилие и компоненты напряжения, если предел текучести материала ![]() кГ/мм2. Поскольку
имеет место двухосное напряженное состояние, напряжение текучести будет
зависеть не только от осевого
кГ/мм2. Поскольку
имеет место двухосное напряженное состояние, напряжение текучести будет
зависеть не только от осевого ![]() и тангенциального
напряжения
и тангенциального
напряжения ![]() , но и от радиального
напряжения
, но и от радиального
напряжения ![]() на внутренней поверхности трубы.
на внутренней поверхности трубы.
Пусть отношение радиального и тангенциального напряжений
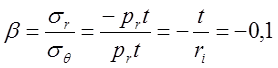 .
.
Решение. Подставив в условие пластичности Мизеса
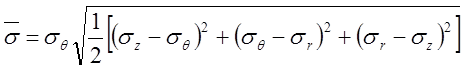
значения напряжений ![]() и
и ![]() ,
выраженных через
,
выраженных через ![]() , получим
, получим
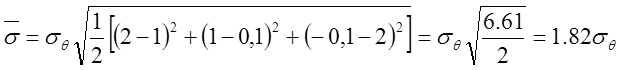 .
.
Поскольку радиальное напряжение изменяется от — ![]() до О, возникновение текучести можно
не заметить до тех пор, пока стенка всей трубы не станет пластичной. Для
условия, когда
до О, возникновение текучести можно
не заметить до тех пор, пока стенка всей трубы не станет пластичной. Для
условия, когда ![]() предполагается равным
нулю,
предполагается равным
нулю, ![]() = 1,73
= 1,73![]() и,
следовательно, ошибка составит 5%. Компоненты напряжения можно получить следующим
образом. Приравнивая предел текучести материала эффективному напряжению, имеем
и,
следовательно, ошибка составит 5%. Компоненты напряжения можно получить следующим
образом. Приравнивая предел текучести материала эффективному напряжению, имеем
![]() кГ/мм
кГ/мм![]()
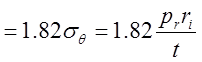 ,
,
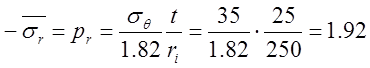 кГ/мм
кГ/мм![]() ,
,
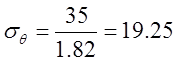 кГ/мм
кГ/мм![]() ,
, ![]() кГ/мм
кГ/мм![]() .
.
Полное усилие растяжения
![]() ,
,
откуда, подставляя значение полученных величин, находим
![]() т.
т.
Если бы было взято условие текучести Треска, тогда
![]() кГ/мм
кГ/мм![]() ,
,
![]() кГ/мм
кГ/мм![]() .
.
6.2. Тонкостенная труба длиной
250 мм имеет толщину стенки 2,5 мм и начальный внешний радиус 50
мм. Пусть зависимость между напряжением и деформацией для этого
материала имеет вид![]() . Труба подвергается
осевому растяжению усилием L и крутящему моменту Т
таким образом, что отношение
. Труба подвергается
осевому растяжению усилием L и крутящему моменту Т
таким образом, что отношение
напряжений  в
любой момент времени. Деформация продолжается до тех пор, пока
в
любой момент времени. Деформация продолжается до тех пор, пока ![]() =17,5 кГ/мм2.
Найти: а) эффективную деформацию в конце процесса деформации; б) конечные
размеры трубы и в) конечную нагрузку и крутящий момент.
=17,5 кГ/мм2.
Найти: а) эффективную деформацию в конце процесса деформации; б) конечные
размеры трубы и в) конечную нагрузку и крутящий момент.
Решение. а) Подстановка  и
и ![]()
![]()
![]()
![]() 0
0
в уравнение (3.27), при
использовании цилиндрических координат и приблизительного равенства ![]() , дает
, дает
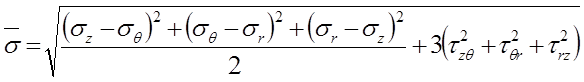 ,
,
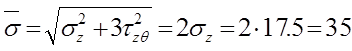 кГ/мм2
кГ/мм2
откуда следует, что
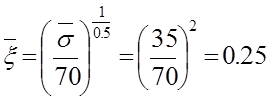 .
.
б) При использовании уравнений пластичности (5.9) в цилиндрических координатах получаем
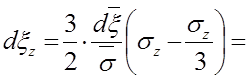
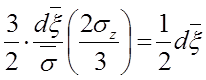 ,
,
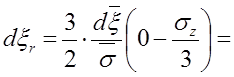
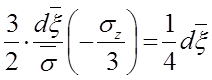 ,
,
отсюда
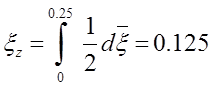 ,
,
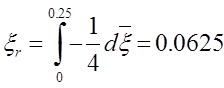 ,
,
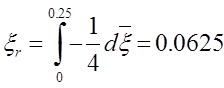
Размеры трубы, вычисленные с помощью уравнения (4,26), следующие:
![]() мм,
мм,
![]() мм,
мм,
![]() мм,
мм,
в) Из уравнения (6.17) для![]() = О
= О
![]() т.
т.
Крутящий момент для равномерного касательного напряжения, действующего на тонкостенное сечение участка А, выражается следующей зависимостью:
![]()
![]()
![]()
![]() кГм.
кГм.
6.3. Тонкостенная труба с
размерами, указанными в задаче 6.2, подвергается Т, так что внутреннему
давлению р, осевому растяжению с усилием L
и крутящему моменту создается постоянное отношение напряжении 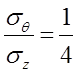 и
и 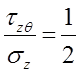 вплоть
до конечного осевого напряжения
вплоть
до конечного осевого напряжения ![]() =35кГ/мм2.
Найти L, р и Т при конечном напряженном состоянии.
=35кГ/мм2.
Найти L, р и Т при конечном напряженном состоянии.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.