Калибровка измерительных цепей. Измерение динамических параметров двухполюсных элементов

2.4.Калибровка измерительных цепей

2.4.1.Измерение динамических параметров двухполюсных элементов

Двухполюсник нужно рассматривать как элементарный многополюсник, который относительно общей шины имеет всего один полюс-вход. В этой связи для определения параметров двухполюсник пригодны как методика измерения, так и расчётные формулы, приведённые для расчёта параметров многополюсника. В донном случае матрица проводимости многополюсника сворачивается до полной проводимости двухполюсник у, которую можно определить с помощью коэффициентов передачи холостого хода  и нагруженной схеме к, которые можно рассчитывать через напряжения холостого хода  , калибровки и нагруженной схеме U.

Согласно рис.2.15 устанавливаем, что методика измерения параметров двухполюсника отвечает условиям измерения параметров i-го входа многополюсника.

Формула для вычисления полной проводимости двухполюсника получаем путём преобразования основной расчётной формулы (2ю39), в которую вместо коэффициентов матриц К0 и К  подставляем коэффициенты передачи  и к, а операции обращения матриц заменяем операциями простого деления.

Тогда

                                                                                                                                  (2.43)

                                            (2.44)

                                    (2.45)

где

                                                      (2.46)

Подставим выражение (2.44) и (2.45) в формулу (2.43), получаем

                                                                                         (2.47)

а)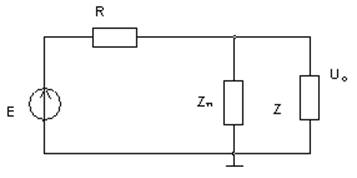                          

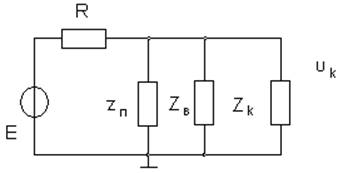
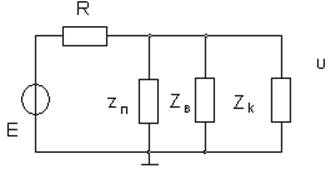
б)                                                                   в)

Рис.2.15.- двухполюсник в измерительной схеме:

а – режим холостого хода; б – режим калибровки;

в – нагруженный режим. или с учётом выражения (2.46)

.                          (2.48)

Выразив отношения напряжений в виде

,                           (2.49)

получаем

                                                 (2.50)

Из формул (2.48) и (2.50) непосредственно следует, что при измерении двухполюсников предложенным методом входное сопротивление измерительного прибора непосредственно на результат определения их полного сопротивления не влияет.

2.4.2.Определение динамических параметров образцовых мер.

Образцовые меры представляют собой двухполюсники, которые подключают к полюсам – входам измерительной схеме при определении компонент вектора калибровочных напряжений Uk. В качестве элементов, с помощью которых моделируются эти меры, удобно применять резисторы. При аттестации параметров этих резисторов необходимо учитывать не только активное сопротивление, но и их реактивную составляющую, которую определяют паразитными параметрами монтажа измерительных цепей. В реальных  случаях реактивную составляющую образцовой меры, моделируемой резистором, непосредственно определить затруднительно из-за сложности определения дополнительного реактивного сопротивления, вносимого монтажными цепями.

Рассмотрим способ калибровки реактивной составляющей образцовой меры . Пусть активная составляющая сопротивления этой меры  известна, например определена с помощью высококачественного моста. Тогда полное сопротивление меры будет равно

                                                     (2.51)

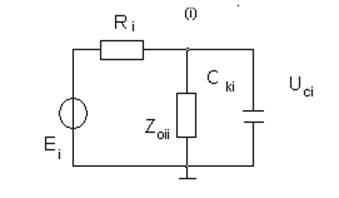
Рис.2.16.- Измерение напряжения  Uci

На первом этапе калибровки выполним операции по измерению полюсных напряжений Uoii  и Uoi . Затем определим напряжение Uci, которое будет вырабатываться на входе i при подключении к нему конденсатора Cki  рис.2.16. Добротность конденсатора должна быть достаточно высокой, чтобы влиянием активных потерь, вносимых им в измерительную цепь конденсатором можно было пренебречь. Полное сопротивление двухполюсника Zci эквивалентного емкости  Cki можно рассчитать по формуле (2.52). В этом случае W рассчитывается по формуле:

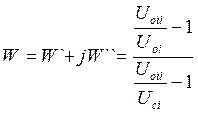                                              (2.52)

где W`- действительна часть коэффициента W;

W – его мнимая часть.

Так как добротность конденсатора Cki высокая, справедливо

                                                     (2.53)

Подставив выражения (2.51) – (2.53) в формулу (2.50), после несложных преобразований получаем

                          (2.54)

Так как по условиям эксперимента действительная составляющая левой части уравнения (2.54) равна нулю, то справедливо