Калибровка измерительных цепей. Измерение динамических параметров двухполюсных элементов, страница 2

                                              (2.55)

Тогда искомую реактивную составляющую Xoi образцовой меры можно определить по формуле

                                                      (2.56)

Если сопротивление Xoi  положительно, то полное сопротивление образцовой меры Zoi  имеет индуктивный характер, и эта мера может быть представлена в виде эквивалентной схемы рис.2.17 а), где Loi – эквивалентная индуктивность меры, значение которой рассчитывается по формуле

                                                         (2.57)

При ёмкостном характере сопротивления Zoi , параметр Xoi  отрицателен, эквивалентную схему образцовой меры можно представить в виде рис.2.16 б), а ёмкость Coi можно рассчитать по формуле

                                                      (2.58)

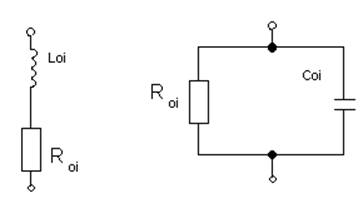
а)                                             б)

Рис.2.17 – Эквивалентные схемы образцовой меры:                                                            а – индуктивного характера; б – ёмкостного характера.

Выражение параметров образцовой меры в виде эквивалентных схем типа рис.2.17 удобно использовать в том случае, когда в рабочем диапазоне частот параметры  Roi, Сoi и Loi можно считать постоянными, т.е. не зависимыми от частоты. В противном случае необходимо экспериментальное определение сопротивлений                  Roi и Xoi на каждой из частот, на которых производится измерение или использовать аналитические  функции Roi и  в заданном диапазоне частот.

Рассмотренный материал отражён в базовых работах (15,51). Развитие метода измерения опубликованы в работах (43-45).

2.4.3.Аттестация паразитных параметров контактно-соединительных                      цепей.

Рассмотрим электрическую цепь измерительной схемы для входа i, представленную на рис.2.17. Измеряемый многополюсник, параметры которого в данном случае отражаются его входным сопротивлением Cii, подключается к измерительной схеме через контакт Xoi рис.2.18 а), а измерительный прибор к точке i`. Между точкой подключения измерительного прибора i` и контактом i имеется монтажный проводник, который в общем случае обладает индуктивностью Li и ёмкостью Ci ,рис.2.18 б). Если преобладает влияние емкости Ci, то оно учитывается при измерении параметров холостого хода, так как непосредственно входит в состав сопротивления  Zoii. В противном случае, когда преобладает влияние индуктивности Li, измеряемое напряжение Uii будет отличаться от напряжения на контакте i, т.е. от напряжения на входемногополюсника (58).

Если паразитный параметр Li известен, то его влияние на результаты измерения может быть учтено. В этой связи возникает задача по определению паразитной индуктивности Li непосредственно в измерительной схеме, так как прямые способы её измерения использовать нельзя.

Такую задачу можно решить путём определения параметров двух двухполюсников, подключаемых к контакту  Xi согласно методике, изложенной в п.2.3.1.

Полное сопротивление двухполюсника Z1 составляют рис.2.18 реактивное сопротивление jXki  индуктивности контакта

                                                         (2.59)

       

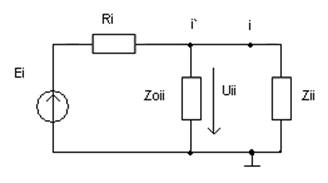
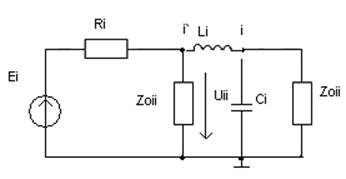
Рис. 2.18. – Изображение измерительной цепи полюса I :

а- принципиальная схема; б – её эквивалент.

               

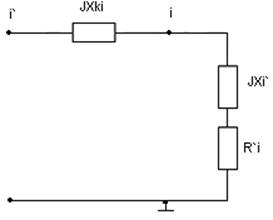
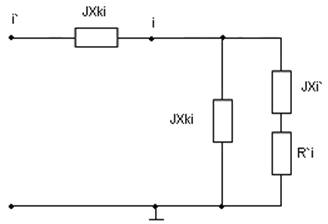
Рис. 2.19. – Тестовые схемы контактных цепей:

а – первая конфигурация; б – вторая конфигурация.

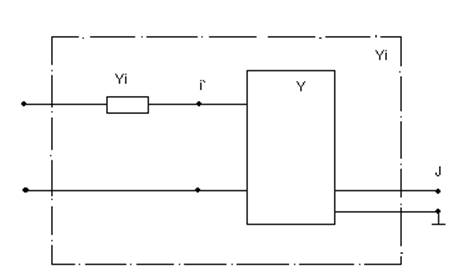
Рис.2.20. – Эквивалентный многополюсник с учётом паразитной проводимости контактного устройства и комплексное сопротивление Z`i  двухполюсника, подключаемого к контакту Xi  

Z`i =R`i+jX`I                                                         (2.60)

В качестве двухполюсника Z`I рекомендуется выбирать резистор. В результате измерения определяются активная и реактивная составляющие сопротивления Z1

Z1=Ri+jXi                                                                                           (2.61) 

Так как сопротивление Z1 определяется параметрами схемы рис. 2.18. а), то справедливо уравнение

                                           (2.62)

Из уравнения (2.62) получаем две формулы

R`i= Ri;                                                                        (2.63)

Z`1=R`i+jX`                                                                  (2.64)

Затем параллельно двухполюснику Z`i  подключается реактивный двухполюсник Z``I, в качестве которого нужно использовать высокодобротный конденсатор. В результате приходим к схеме рис.2.18 б). В результате измерения параметров схемы, образуемой индуктивностью и мнимую части двухполюсника