Z2=R2+jX2 (2.65)
Теоретическое выражение сопротивления Z2 через параметры схемы рис.2.18б) имеет вид
![]() (2.66)
(2.66)
Преобразовав формулу (2.66) с учётом выражений (2.63) и (2.64), получаем
![]() (2.67)
(2.67)
Из выражений (2.65) и (2.66) после несложных преобразований приходим к двум уравнениям
![]() ;
(2.68)
;
(2.68)
![]() (2.69)
(2.69)
решая которые относительно параметра ![]() получаем
получаем
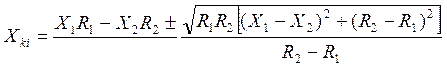 (2.70)
(2.70)
Из формулы (2.70) непосредственно находим основное расчётное уравнение для определения индуктивности контакта
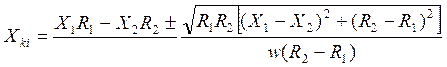 (2.71)
(2.71)
2.4.4.Корректировка Y – матриц по данным аттестации контактно-соединительных цепей
Влияние соединительного проводника, показанного в виде индуктивности на рис. 2.18,б).
Влияние индуктивности Li проявляется в том, что истинный вход i объекта измерения – многополюсника Y , превращается во внутренний узел многополюсника Y`. Коэффициенты матрицы Y` будут отличаться от коэффициентов матрицы Y тем больше чем , сильнее будет нарушено условие
![]() (2.72)
(2.72)
где ![]() - модуль входного
сопротивления многополюсника Y со стороной полюса i.
- модуль входного
сопротивления многополюсника Y со стороной полюса i.
Чтобы определить связь коэффициентов матриц Y и Y`, которые имеют размер n, рассмотрим структуру матрицы Y`` размером n+1 с дополнительным узлом i` рис.2.19. Согласно правилам формирования матриц проводимости элементы матрицы Y`` можно определить через элементы матрицы Y и проводимость Yi по формулам
![]() (2.73)
(2.73)
![]() (2.74)
(2.74)
![]() (2.75)
(2.75)
![]() (2.76)
(2.76)
![]() (2.77)
(2.77)
![]() (2.78)
(2.78)
Тогда матрица Y`` может быть выражена в виде
![]()
![]()
![]()
![]()
![]() Y11 ... Yli``=0 … Yln Y``li`=Yli
Y11 ... Yli``=0 … Yln Y``li`=Yli
Yil``=0 … Yii``=Yi … Yin Yii``=-Yi
Y``= … … … … … … (2.79)
![]()
![]() Yi`l``=Yil ... Yi`i``=-Yi … Yi`i``=-Yin Yi`i``=Yii+Y
Yi`l``=Yil ... Yi`i``=-Yi … Yi`i``=-Yin Yi`i``=Yii+Y
Где Yij,i=1, n;j=1,n – элементы матрицы Y.
Чтобы преобразовать матрицу Y`` в матрицу Y` , необходимо выполнить её редукцию, исключив узел i`. Воспользовавшись рекуррентной формулой Гаусса
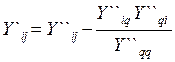 (2.80)
(2.80)
где q - индекс исключаемого узла; при q=i` из (2.204) получаем следующие расчётные формулы для коэффициентов матрицы Y`
![]() (2.81)
(2.81)
![]() (2.82)
(2.82)
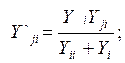 (2.83)
(2.83)
![]() (2.84)
(2.84)
Из уравнений (2.81)-(2.84) приходим к алгоритму определения коэффициентов искомой матрицы многополюсника Y через коэффициенты матрицы Y`, которые вычисляются по результатам измерения:
1) находим узловую проводимость корректируемого узла, воспользовавшись выражением (2.82)
![]() (2.85)
(2.85)
2) используя выражений (2.83) и (2.84) с учётом формулы (2.210) определяем коэффициенты взаимной проводимости
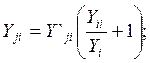 (2.86)
(2.86)
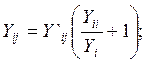 (2.87)
(2.87)
используя данные расчёта по формулам (2.85)-(2.87) определяем остальные коэффициенты при k,j≠i
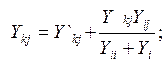 (2.88)
(2.88)
Таким образом, применяя формулы (2.85)-(2.88), можно скорректировать влияние индуктивности контакта на результаты измерения для любого из входов-полюсов измерительной схемы. В общем случае такая операция должна производится nраз (по числу полюсов). Для оптимизации вычислительного процесса желательно в каждом случае обосновать необходимость такой корректировки. Это может быть произведено в результате анализа конкретных значений индуктивности Li, влияние которых возрастает с частотой. В первом приближении этим влиянием можно пренебречь, если выполняется условие (2.72).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.