Математические модели транзисторов. Макромодели биполярных транзисторов

современных САПР электронных схем, например, PSpice широко используются встроенные модели. В системе PSpice в состав этих моделей входят модели диода, биполярного транзистора, канального полевого транзистора, МОП-транзистора и магнитного сердечника. Указанные модели позволяют рассчитывать статические линейные и нелинейные динамические режимы. В основу моделей диодов и транзисторов положены идеи выдвинутые Эберсом и Моллом. В этих моделях отражены достижения последних десятилетий.

К достоинствам встроенных моделей  можно отнести:

-  элементы, указанные выше, можно аттестовать по справочным данным;

-  в зависимости от решаемой задачи можно определить уровень сложности моделей, тем самым оптимизируя процесс вычисления;

-  для МОП транзистора предлагается 4 уровня сложности, а для биполярного транзистора 3, кроме моделей Гуммеля-Пунна аттестуемой 59 параметрами и константами.

Также предусмотрены усеченное использование моделей Эберса-Молла на основе 16-20 параметров, предоставление пользователю корректировки встроенных моделей.

К недостаткам встроенных моделей, приведенных в литературе /2/ следует отнести их сложность. Анализ показывает, что для расчета малосигнальной модели биполярного транзистора требуется использовать практически весь математический аппарат нелинейного варианта его модели. 

Также к недостаткам следует отнести ограниченный частотный диапазон. По данным /2/ частотный диапазон биполярного транзистора ограничен 100 МГц. Отсутствие достаточного объема справочной информации и связанной с этим необходимость организации сбора дополнительной информации, путем реализации дополнительных измерительных процессов.

В современных САПР электронных схем, как правило, БТ моделируют с помощью передаточной модели Эберса-Молла в версиях Логана /1/ и Гуммеля-Пуна. В этом случае, в качестве основных токов используются токи, собираемые p-n-переходам. Эти токи в эквивалентной схеме моделируются генераторами тока.

Ток, который передается из эммитера в базу и собирается коллектором, описывается следующим выражением:

Аналогично записывается выражение для тока, который передается из коллектора через базу в эмиттер:

где IS – ток “отсечки”.

Из (2.1) и (2.2) видно, что основные токи передаточной модели описываются выражениями с одним параметром  IS, требующим измерений. Для описания основных токов инжекционной разновидности модели необходимо измерить четыре параметра: 

В цепь базы транзистора ответвляется ток

где βN и βI – нормальный и инверсный коэффициенты передачи в схеме включения с общим эмиттером. Токи через выводы эмиттера и коллектора имеют вид

Эквивалентная схема передаточной модели Эберса-Молла, соответствующая уравнениям (2.1) – (2.5), приведена на рис. подключаются барьерные и диффузионные емкости. Барьерные емкости зависят от напряжений на переходах по формуле (2.8) и по сравнению с инжекционным вариантом модели и не имеют никаких отличий.

Диффузионные емкости зависят от основных токов по следующим формулам:

где τ N , τI – диффузионные постоянные времени в нормальном и инверсном включении.

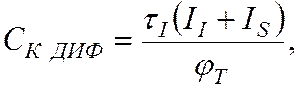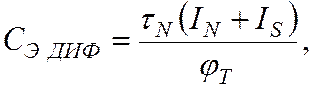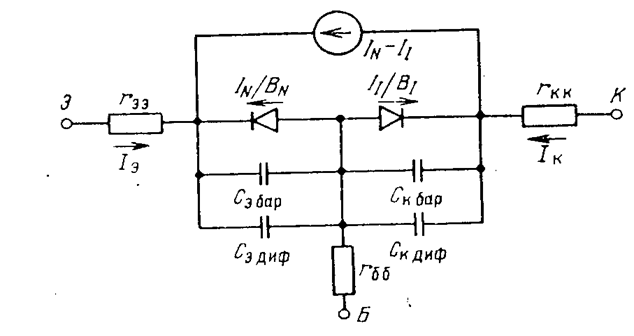Рисунок 2.2- Эквивалентная схема передаточной модели Эберса-Молла

Отметим, что постоянные времени τNи τI характеризуют инерционность процессов передачи зарядов неосновных носителей от одного перехода к другому, в то время как постоянные времени ταN , ταIинжекционного варианта характеризуют инерционность не только процессов передачи носителей заряда, но и процессов их рекомбинации у соответствующих переходов.

Барьерная емкость нелинейно зависит от напряжения и приближенно описывается выражением

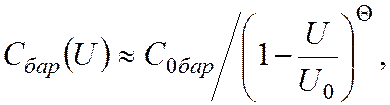где C0бар – барьерная емкость   p-n-перехода при нулевом смещении