ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ
И ОСЕСИММЕТРИЧНАЯ ДЕФОРМАЦИЯ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1. Доказать, что в области, которая находится рядом о областью равномерного' поля напряжений, поле напряжений всегда является простым.
Решение. Поле напряжений, в
котором одно семейство линий скольжения (например, ![]() )
состоит из прямых линий, называется простым. Если в некоторой области
прямолинейны оба семейства линий скольжения, то в этой области постоянны
параметры
)
состоит из прямых линий, называется простым. Если в некоторой области
прямолинейны оба семейства линий скольжения, то в этой области постоянны
параметры ![]() и
и ![]() и
напряжения распределены равномерно. Такое поле напряжений называют равномерным
[12].
и
напряжения распределены равномерно. Такое поле напряжений называют равномерным
[12].
Пусть в области А
(рис. 49) имеем равномерное поле напряжений, т. е. в этой области линиями скольжения
является сетка взаимно перпендикулярных прямых. Обозначим для семейств линий
скольжения ![]() и
и ![]() параметры
параметры![]() и
и ![]() ответственно через
ответственно через
![]() и
и ![]() .
Предположим, что прямая L является границей
области А. Поскольку эта прямая принадлежит также и соседней с областью А
области В и является линией скольжения в ней, то используем следствие из
первой теоремы Генки: если некоторый отрезок линии скольжения одного из
семейств — прямой, то все соответствующие отрезки линий этого семейства,
отсекаемые линиями второго семейства,— прямые., Следовательно, в области В
одно семейство линий скольжения (например,
.
Предположим, что прямая L является границей
области А. Поскольку эта прямая принадлежит также и соседней с областью А
области В и является линией скольжения в ней, то используем следствие из
первой теоремы Генки: если некоторый отрезок линии скольжения одного из
семейств — прямой, то все соответствующие отрезки линий этого семейства,
отсекаемые линиями второго семейства,— прямые., Следовательно, в области В
одно семейство линий скольжения (например, ![]() )
состоит из прямых линий и поле напряжений в области В является простым.
Значение параметра
)
состоит из прямых линий и поле напряжений в области В является простым.
Значение параметра ![]() для семейства
линий скольжения
для семейства
линий скольжения ![]() в области В такое
же, как и в области А, т. е.
в области В такое
же, как и в области А, т. е. ![]() .
.
2. Определить осесимметричное состояние при отсутствии скручивания для бесконечной пластины с круговым вырезом.
Решение. Поскольку скручивание отсутствует, то ![]() . Компоненты
. Компоненты
же ![]() и
и
![]() будут главными напряжениями. Если по
контуру выреза R = а (рис. 50) I действует внутреннее
давление, а на бесконечности напряжения равны нулю, то вблизи отверстия
будут главными напряжениями. Если по
контуру выреза R = а (рис. 50) I действует внутреннее
давление, а на бесконечности напряжения равны нулю, то вблизи отверстия ![]() <0,
<0, ![]() >
0 и решение будет таким же, как и для случая плоской деформации. |
>
0 и решение будет таким же, как и для случая плоской деформации. |
Если же пластина со свободным вырезом испытывает на
бесконечности равномерное растяжение, то напряжения ![]() и
и ![]() имеют
один и тот же знак и условие текучести
имеют
один и тот же знак и условие текучести
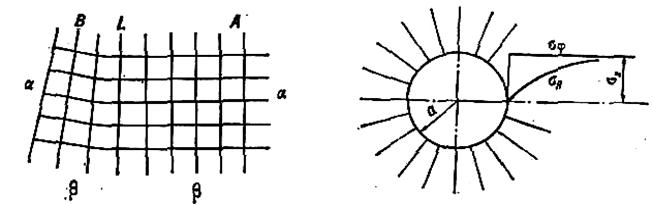 Рис. 49 Линии скольжения
в Рис. 50. Линии скольжения в
Рис. 49 Линии скольжения
в Рис. 50. Линии скольжения в
равномерном (а) и простом (В) бесконечной пластине с круго
полях напряжений вым вырезом
(6.13) имеет вид ![]() =
const =
=
const = ![]() . Тогда из первого уравнения
равновесия (8.18) при
. Тогда из первого уравнения
равновесия (8.18) при ![]() и граничном условии
и граничном условии ![]() при R = 0 получим
при R = 0 получим
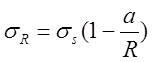 .
.
Эта задача относится к параболическому типу и единственное семейство характеристик представляет пучок прямых, исходящих из центра (рис. 60). На рис. 60s также показано распределение напряжений.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.