


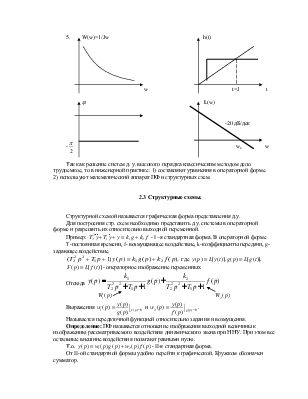





Лекция №2.
2.1 Управления движения ЭП. Математическая модель механической части.
Итак, механическая часть ЭП сводится чаще всего к 2х массовой расчетной схеме.
ПМ Мс с12
![]()

![]()
![]()
![]()

![]()
![]()
![]()
![]()


 w1 w2
w1 w2
![]()
![]()
![]() РД ИМ => J1 J2
РД ИМ => J1 J2
![]() М
М ![]()
![]()
![]() ,w1
,w1
![]()
![]() M
M ![]() ,w1
,w1
![]()
![]() My My
My My
![]() Mc
Mc
Электромагнитный момент будем
рассматривать как управляющее воздействие, а скорости валов w1
и w2 – как регулируемые координаты (или
положения валов ![]() и
и ![]() ).
).
При управлении механической частью решается одна из двух задач.
1)
прямая задача динамики. Дано: M(t). закон -> найти w1(t) и w2(t),
а лучше ![]() и
и ![]() .
.
2)
обратная задача динамики. Дано: ![]() (t) и w2(t)
-> найти
(t) и w2(t)
-> найти ![]() (t)
или w2(t) и M(t).
(t)
или w2(t) и M(t).
Для решения этих задач во-первых, нужна расчетная схема, отражающая динамические свойства механической части системы, во-вторых, нужна математическая модель системы, т.е. уравнения, связывающие M(t) с w1(t) и w2(t), или уравнения динамики системы. Их получают путем составления уравнения Лагранжа.
![]()
Здесь qi – это обобщенная координата системы
![]() - обобщенная скорость.
- обобщенная скорость.
Qi – обобщенная сила
Wk – кинетическая энергия системы.
qi=![]() ,
, ![]() = w1,
q2=
= w1,
q2=![]() ,
,
![]() .
.
Q1
находится с помощью элементарной работы всех сил, действующих на элементарном
перемещении по данной координате: ![]()
Механическая часть ЭП сводится
чаще всего к 2-массовой расчетной схеме. Зададим (+) направления вращения масс
и укажем все действующие моменты. Составим для расчетной схемы уравнения
Лагранжа. В качестве обобщенных координат используем угловые координаты масс ![]() и
и ![]() .
.
Кинетическая энергия системы. 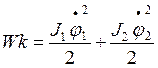 .
.
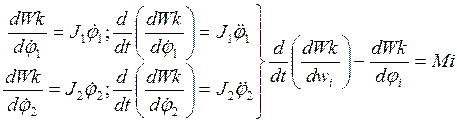
Поскольку Wk
не зависит от ![]() и
и ![]() , то
, то
![]()
Элементарная работа при
приращении:![]()
Составляем уравнения:
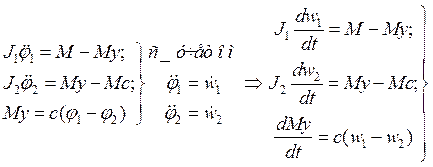 - это форму
используют чаще.
- это форму
используют чаще.
![]() -
уравнение статики, его нельзя решать совместно с уравнениями динамики.
-
уравнение статики, его нельзя решать совместно с уравнениями динамики.
Итак, 2-массовая схема описывается системой диф. уравнений как минимум третьего порядка, т.е. достаточна сложна для инженерных расчетов.
Поэтому на практике стремятся
свести систему к одномассовой расчетной схеме, т.е. полагают, что массы
соединены абсолютно жестким валом: ![]() . В
каких случаях это допустима? Вопрос сложных и для точного ответа требует
специальных расчетов для каждого конкретного случая. “На глазок” жесткость
редуктора или соединительной муфты не измеришь. Но если массы соединены просто
стальным валом, то есть простой инженерный критерий: упругость вала нужно
учитывать, если отношение длины вала к диаметру больше 20. На практике это
бывает не часто.
. В
каких случаях это допустима? Вопрос сложных и для точного ответа требует
специальных расчетов для каждого конкретного случая. “На глазок” жесткость
редуктора или соединительной муфты не измеришь. Но если массы соединены просто
стальным валом, то есть простой инженерный критерий: упругость вала нужно
учитывать, если отношение длины вала к диаметру больше 20. На практике это
бывает не часто.
![]()
![]() 200
200
![]() D=10
D=10
![]() -модуль Юнга ля стали.
-модуль Юнга ля стали.![]()
![]() среза – одномассовая схема.
среза – одномассовая схема.
Итак, в случае абсолютно жесткого
вала ![]() , w1=w2=w и
уравнения приобретают вид.
, w1=w2=w и
уравнения приобретают вид.
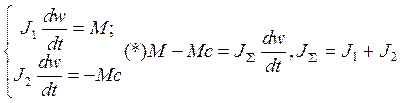
Одномассовую расчетную схему и уравнение (*) мы будем использовать чаще всего.
Итак, получены уравнения динамики 2-массовой и 1-массовой расчетных схем механики ЭП. В принципе с их помощью можно решать прямую и обратную задачи динамики.
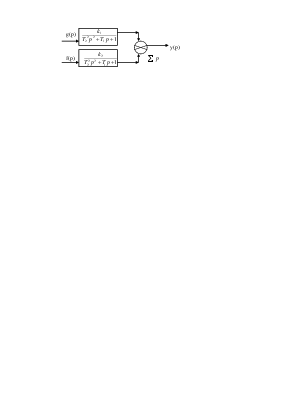
2.2 Математические методы анализа динамики ЭП.
Прямая задача динамики. реальное устройство
![]() Дано: воздействие g(t) (сила, момент)
Дано: воздействие g(t) (сила, момент)
![]() Найти: реакцию y(t) (перемещение,
скорость) расчетная схема
Найти: реакцию y(t) (перемещение,
скорость) расчетная схема
![]()
![]() y,g
y,g
![]()
![]()
![]()
![]() мат. модель (д. у.)
мат. модель (д. у.)
![]() g=1(t)
структурная схема и ПФ
g=1(t)
структурная схема и ПФ
 частотные характеристики
частотные характеристики
y(t)-?
W(w),L(w),![]()
перех. характеристика
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.