t h(t)
Пример: ротор ЭД
1. J
![]()
![]()
![]()
![]()
![]()
![]() Возд. g(t)=M0*1(t)
Возд. g(t)=M0*1(t)
Реакц. y(t)=w(t)
![]()
![]()
![]()
M Mc w
![]()
2. Расчетная схема отображает существенные для анализа динамики свойства исследуемого устройства. В данном случае это цилиндр, который вращается вокруг оси со скоростью w под действием электромагнитного момента М и тормозного момента Мс.
3. Уравнение Лагранжа.
![]() Введем обозначения.
Введем обозначения. ![]() , тогда
, тогда ![]() , а
, а ![]() . Получим
. Получим ![]()
4. Д.у. в операторной форме (применяем преобразования Лапласа).
w(p)=L[w(t)] Если функцию времени f(t) изобразить функцией F(p) комплексной переменной. ![]() ,
то диф. ур. для F(p)
соответствует алгебраическое уравнение для F(p). Решить его проще.
,
то диф. ур. для F(p)
соответствует алгебраическое уравнение для F(p). Решить его проще.
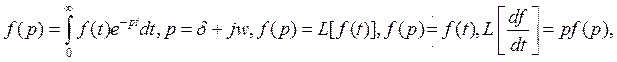
![]() .
.
![]() . При wc(p)=0 – это интегральное звено. ПФ:
. При wc(p)=0 – это интегральное звено. ПФ: ![]()
Структурная схема.
М(р)
 w(p)
w(p)
![]()
![]()
![]()
![]()
![]()
![]()
- ![]() Mc
Mc
![]()
![]()
![]()
![]()
![]()
![]()
![]() 5. W(w)=1/Jw h(t)
5. W(w)=1/Jw h(t)
 |
 |
||
w t=J t

![]() L(w)
L(w)
-20 дБ/дек
![]()
![]() -
-![]() wc w
wc w
Так как решение систем д. у. высокого порядка классическим методом дело трудоемкое, то в инженерной практике: 1) составляют уравнения в операторной форме.
2) используют математический аппарат ПФ и структурных схем.
2.3 Структурные схемы.
Структурной схемой называется графическая форма представления д.у.
Для построения стр. схем необходимо представить д.у. системы в операторной форме и разрешить их относительно выходной переменной.
Пример: ![]() - I
–я стандартная форма. В операторной форме
- I
–я стандартная форма. В операторной форме
T-постоянная времени, f- возмущающее воздействие, k-коэффициенты передачи, g-задающее воздействие.
![]() где
где
![]()
![]() -
операторное изображение переменных.
-
операторное изображение переменных.
![]()
![]() Отсюда
Отсюда 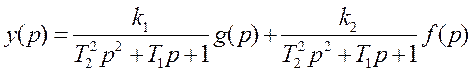
![]()
![]()
Выражения ![]() и
и ![]() .
.
Называется передаточной функцией относительно задания и возмущения.
Определение: ПФ называется отношение изображения выходной величины к изображению рассматриваемого воздействия динамического звена при ННУ. При этом все остальные внешние воздействия полагают равными нулю.
Т.о. ![]() -
II-я стандартная форма.
-
II-я стандартная форма.
От II-ой стандартной формы удобно перейти к графической. Кружком обозначен сумматор.
![]()
![]()
![]()
![]()
 g(p)
g(p)
![]()
![]()
![]()
![]()
 y(p)
y(p)
![]()
![]()
![]() f(p)
f(p) ![]()
![]()
2.4 Динамические звенья.
При расчете систем ЭП их обычно
разбивают на отдельные динамические звенья. Под д.з. понимают устройство
физического вида, движение которого описывается определенным уравнением
движения. ![]() , у-вых, g-
вх. координаты.
, у-вых, g-
вх. координаты.
 Обозначение д.з.
Обозначение д.з.
![]()
![]() g1(p)
g1(p)
![]()
![]() g1(p)
g1(p)
 |
![]()
![]() W(p) y(p)
W(p) y(p)
W(p) y(p)
W(p) y(p)
![]() g2(p)
gn(p)
g2(p)
gn(p)
g1=M, g2=Mc, y=w
Пример: представим в форме ж.з. одномассовую расчетную схему.
 |
||||
![]()
w
M
Mc
Первая стандартная форма. ![]()
В операторной форме ![]()
Вторая стандартная форма ![]() , где
, где ![]() ,
,![]()
Построим теперь структурную схему двухмассовой расчетной схемы. Ее уравнения в интегральной форме имеют вид. Пологая Мс1=0, Мс2=Мс.
![]()
![]()
![]()
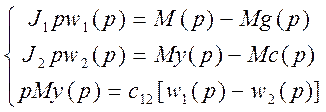 Каждому из трех уравнений
соответствует свое динамическое звено, выразим уравнения в стандартной форме,
удобной для сост. стр. схемы.
Каждому из трех уравнений
соответствует свое динамическое звено, выразим уравнения в стандартной форме,
удобной для сост. стр. схемы.
 |
|||||||||||
 |
 |
 |
 |
 |
|||||||
![]()
![]()
![]()
![]()
![]()
![]()
![]() М(р)
w1(p) -w2(p)
My(p) w2(p)
М(р)
w1(p) -w2(p)
My(p) w2(p)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() -
-
![]()
![]()
![]()
![]() My(p)
My(p)
Мс
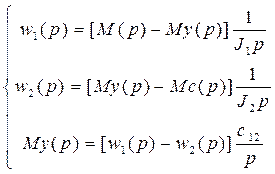
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.