Графическая интепритация системы д.y в виде структурной схемы нагляднее, чем их аналитическая запись. Но главное на основе аппарата структурных схем и ПФ разработаны методы, позволяющие решать задачи динамики в ЭП без решения диф. уравнений.
2.5 Характеристики динамических звеньев.
Свойства динамического звена полностью определяются его передаточной функцией (ПФ), т.е. мы имеем в виду, что зная ПФ можно определить реакцию звена y(t) на различные воздействия g(t). Инженера чаще всего интересуют реакция звена на два вида воздействий.
1) 
-
установившийся режим.
Связь межу ym->gm 
выражает ЧХ.
 |
2)
?
Эта связь выражается временными характеристиками. Переходный процесс, т.е. динамическая характеристика. Т.о. д.з. характеризуется ЧХ-ми и временными.
2.5.1 Частотные характеристики д.з..
-
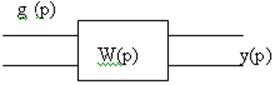
будет на выходе звена.
Амплитуда ym(w) и фаза
,
зависят от w.
Частотные характеристики.
1) АЧХ 
2) ФЧХ 
3) КЧХ или АФЧХ
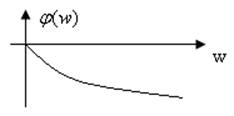
JV
J
 |
w=
w=0 U
gm
w
1
W(w)
КЧХ в полной мере определяет динамические свойства звена. Может быть получена
.
2.5.2 Логарифмические частотные характеристики.
В ЭП (а также в автомобиле, радиотехнике и др.) ЧХ часто строят в логарифмическом масштабе, т.е. при изображении логарифмами чисел операции над ними упрощаются. Умножение и деление заменяются на сложение и вычитание, операции над функциями становятся проще.
1) 
2) y1=kx2,
y2=kx3, 
, 
lgy lgy2
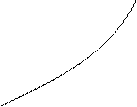
y
y2 y1
lgy1
x
lgx
3) 
4)
Степенные и показательные функции при логарифмировании замещаются линейными с прямыми графиками. Чем больше показатель степени, тем круче наклон прямой в лог. масштабе.
2.5.2.1. ЛАХ.
Это также АЧХ, но построенная в другой системе координат.
Декада – единица частоты в ЛЧХ, это интервал, на котором частота уменьшится в 10 раз.
усиление L(w),дБ
20
10
1 2 3 lgw
l(w)=0
0.1 1 2 10
100 1000 w,[p/c]
 |
 |
октава декада ослабление
Начало координат помещ. в точке w=1, т.к. lg1=0. Точка w=0 лежит в бесконечности. Однако можно начало координат брать в другой точке 0.1, 10…
Вдоль оси абсцисс откладываются сами частоты в рад/с, поэтому шкала частот неравномерна.
По оси ординат откладываются ФЧХ, выраженные в децибелах.
2.5.2.2 ЛФХ.
ЛФХ – это ФЧХ 
звена, построенная в таком
же масштабе частот, что и L(w).
Изменению W(w) в 10 раз
соответствует изменение L(w) на
20 дБ.
Удобный масштаб оси частот – 5 см/дек.
Оси ординат 1:1 – 1дБ - 1мм.
2.5.3 Временные характеристики динамических звеньев.
Временные характеристики – это реакция звена на входное воздействие стандартной формы. Под реакцией понимается форма переходного процесса на выходе звена. Рассмотрим лишь одну в.х., наиболее важную, т.н. переходную характеристику (ПХ) h(t):
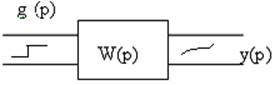g(t)=1(t), 
Переходная характеристика – это реакция цепи на единичную функцию при ННУ.
.
АЧХ и ФЧХ – это статическая характеристика – связь устан-ся значений y=f(g). В.Х. – это форма переходного процесса. Это динамическая характеристика, т.е. функция времени.
Переходная характеристика определяется ПФ-ей звена. Изображение по Лапласу единичной функции. L[1(t)]=1/p.
Изображение переходной
характеристики обозначит H(p)=L[h(t)].
Очевидно, оно равно 
- тоже полезно.
Пользуясь этим, находят переходные характеристики по ПФ,
.
Знание ПХ позволяет найти реакцию звена на воздействие g(t) произвольной формы.
Пусть дано: g(t), h(t). Найти y(t)-?
С помощью интеграла Дюамеля
найдем: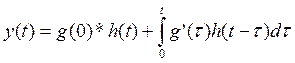 
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.