Магнитний момент струму.
Застосуємо Закон Біо-Савара для визначення магнітного поля, що створене кільцевим струмом.
Рис.
![]() dl=adj
dl=adj
![]()
![]()
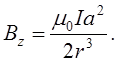 В центрі витка r=a і ми маємо
В центрі витка r=a і ми маємо ![]()
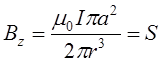
![]()
![]() - магнітний момент струму. Можна показати, що на
далеких відстанях від довільного контура струму (r>>a) магнітна індукція буде
- магнітний момент струму. Можна показати, що на
далеких відстанях від довільного контура струму (r>>a) магнітна індукція буде
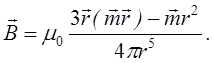
Таким чином, існує аналогія між дипольним моментом і магнітним моментом.
Ампер ввів терміни: електродинаміка, е.р.с., напруга, гальванометр, соленоїд
На елемент провідника ![]() зі струмом I1 з боку струму I діє сила
зі струмом I1 з боку струму I діє сила
![]()
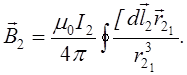
Такоим чином, закон Ампера має вигляд
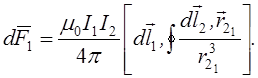
Нехай струм I2 тече L2 вздовж дуже довгого прямолінійного провідника. Тоді
![]()
![]() - одиничний
вектор вздовж провідника зі струмом I2, r – відстань між
- одиничний
вектор вздовж провідника зі струмом I2, r – відстань між ![]() та другим провідником, причому
та другим провідником, причому ![]() дівиться до
дівиться до ![]()
![]()
![]() і вважаючи,
що
і вважаючи,
що ![]() маємо
маємо
![]()
![]()
Потенціальна функція струму в магнітному полі
Нехай контур
зі струмом, що знаходиться в магнітному полі, трохи змістився під дією сил (та
ще й деформувався). Якщо елемент контура ![]() змістився
на відрізок
змістився
на відрізок ![]() то робота сили
то робота сили ![]() є
є
![]()
Але ![]() - вектор площини, що описав
вектор
- вектор площини, що описав
вектор ![]() при його зміщенні на
при його зміщенні на ![]() тому
тому
Рис.
![]()
![]()
Роботу сил можна виразити через магнітний потік
![]()
Оскільки магнітних зарядів немає, то
![]()
![]()
![]()
![]()
![]() та
та ![]() направлені
по зовнішній нормалі, а
направлені
по зовнішній нормалі, а ![]() - по
внутрішній (правило обходу дає правий гвинт!)
- по
внутрішній (правило обходу дає правий гвинт!)
![]()
![]()
![]()
Хоча магнітне поле не є потенціальним, можно ввести потенціальну функцію струму у магнітному полі, зменшення якої визначить роботу, що виконують сили поля
![]() так що
так що
![]()
Приклад: Рамка зі струмом.
![]()
![]()
Момент сил
![]()
![]()
Сила намагається зробити v=0, щоб U=Umin.
Визначимо тепер потенціальну функцію двох струмів I1 та I2. Функція U12 струму I1 в магнітному полі B(*), що створюється струмом I2 є
![]()
де ![]() - магнітний потік, що
створюється струмом I2 і пронизує контур
струму I1 . Оскільки B(*)~I2, то й потік
F21~I2 , тобто
- магнітний потік, що
створюється струмом I2 і пронизує контур
струму I1 . Оскільки B(*)~I2, то й потік
F21~I2 , тобто
F21=L21I2,
де L21 – коефіцієнт, що залежить тільки від геометрії контурів та їх взаємного розташування. Його називають взаємною індуктивністю контурів
![]()
Аналогічно
![]()
Але має виконуватись рівність дії і протидії, значить
![]()
Для тонких проводів:
![]()
![]()
![]()
А для лінійних провідників
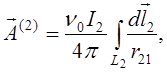
![]() - відстань між
- відстань між ![]() та
та ![]()
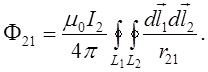
Звідси
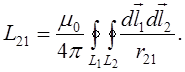
L12 може бути >0, <0, або =0.
Разом з взаємною потенціальною функцією ми повинні ввести власні потенціальні функції U11 та U22 . Покажемо, що
![]()
Для цього розіб`ємо струм I1 на тонкі нитки струму DI1 . Тоді DU11 якоїсь нитки DI1 в полі решта струмуI1-DI1 буде DU11=DI1F11-
DI1®0.
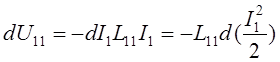
![]()
Аналогічно
![]()
Сумарна функція
![]()
![]()
Приклад. Індуктивність соленоїда (довгий і тонкий)
![]()
Магнітний потік
через один виток BS=m0nSI. Помножимо
це на загальне число витків N, F=m0nNSI.
Прирівняємо це до LI, L=m0nNSI або ![]()
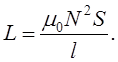
Знайдемо тепер власну потенціальну функцію соленоїда
![]()
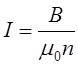
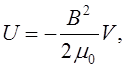
![]()
Розглянемо тепер соленоїд з двома обмотками, що мають N1 та N2 витків і нехай по них течуть струми I1 та I2 . Знайдемо L12 ?
I2®B(2)=m0n2I2
Його магнітний потік SB(2)=m0n2SI2. Помножимо це на загальне число витків першої обмотки N1, знайдемо
F21=m0n2SN1I2«F21=L12I2
L12=m0n2SN1 (±)
(+) – коли I1, I2 в одному напрямку
(-) – коли I1, I2 в протилежному напрямку
![]()
L12=±m0n1n2
![]()
Сума:
![]()
m0n1I1=B(1), m0n2I2=B(2),
L12=±m0n1n2V, L1=±n12V, L2=m0n22V
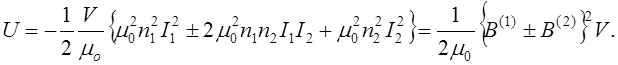
Одиниці в СІ: [F]=1 Вб =1 В×сек, [B]=1 Тл =1 Вб/м2, [L]=1 Гн =1 Вб/А-1
Існує ще одна можливість для магнітного поля: силова лінія, не маючи ні початку, ні кінця, щільно заповнює цілу поверхню, яка має назву магнітної поверхні.
Оскільки струм створює навколо себе магнітне поле, то, як вже значилось, два струми взаємодіють один з другим електродинамічно.
На елемент провідника ![]() зі струмом I1 з боку струму I2 діє сила
зі струмом I1 з боку струму I2 діє сила
![]()
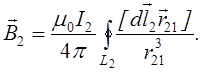
Таким чином,
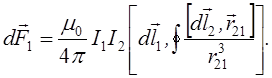
Це закон Ампера.
Розглянемо випадок, коли струм I2 тече вздовж дуже довгого прямолінійного провідника, тоді
![]()
![]()
![]() -
одиничний вектор, направлений вздовж провідника зі струмом I2 ;
-
одиничний вектор, направлений вздовж провідника зі струмом I2 ;
![]() -
відстань між
-
відстань між ![]() та другим провідником причому
та другим провідником причому ![]() - направлений від другого
провідника до
- направлений від другого
провідника до ![]()
![]()
![]() і
вважаючи
і
вважаючи ![]() маємо,
маємо,
![]()
![]()
![]()
![]()
![]()
Рис.
![]()
Рис.
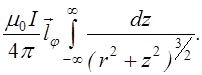 |
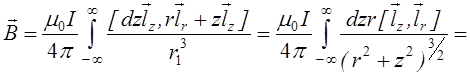
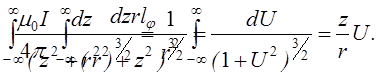 |
![]()
![]()
![]()
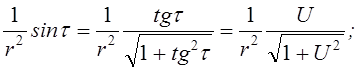
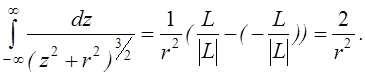 |
![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.