ЕРС взаємної та самоіндукції. Індуктивність і ємність в ланцюгу змінного струму

Лекція 9

Е.р.с. взаємної та самоіндукції

Рис.

Нехай у першому контурі діє змінна в часі електрорушійна сила та тече змінний струм. Тоді від часу залежить і  що створюється струмом  а значить, і магнітний потік F₂₁, що пронизує другий контур і створюється струмом в першому контурі. Значить, в другому контурі виникає е.р.с. індукції

Це е.р.с. взаємної індукції.

Для постійних струмів ми показали, що F₂₁=L₂₁i₁. Виявляється, що такими самими формулами можна користуватись і для змінних струмів, для яких справедливо наступне:

Час, за який струм змінюється, має бути великим, порівняно з часом, який потрібен світлу, щоб подалати відстань між контурами, а також відстань порядку розмірів самих контурів

Такі струми називаються квазістаціонарними.

Е.р.с. взаємної індукції виникне в контурі 2 струм i₂ ,який, як i₁ , буде змінним. Тому він, в свою чергу, викличе в контурі 1 е.р.с. взаємної індукції

Окрім того, виникнуть ще дві е.р.с. індукці, звязані зі зміною власних магнітних потоків F₁₁ та F₂₂

F₁₁=L₁i₁,   F₂₂=L₂i₂,

а саме

Таким чином, в контурі 1:

а в контурі 2:

Індуктивність і ємність в ланцюгу змінного струму

Рис.

Якби е=const, ми б мали  але є період включення постійного струму. Як він протікає?

Виявляється, що струм стає постійним на зразу, адже спочатку струму не було зовсім. Зміна струму викличе е.р.с. самоіндукції  так що в контурі діятимуть дві е.р.с. (постійна і е.р.с. самоіндукції)

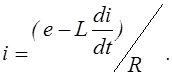
це - диференціальне рівняння першого порядку. Воно розв`язується так. Загальний розв’язок є сума загального розв’язку рівняння без правої частини + частковий розв’язок рівняння з правою частиною.

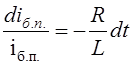
Початкова умова:

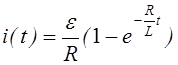
Рис.

Нехай тепер

Застосуємо комплексний метод

I – комплексна амплітуда.

Беручи e(t)=R_eUe^iwt, маємо

z – імпеданс z=R+iwL.

Зовнішне джерело е.р.с. дає за dt в ланцюг енергію

Ri²>0, а 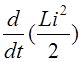 може бути >0 і <0.

Дійсно

I=Icos(wt-j), i²=I²cos²(wt-j)

Магнітна енергія неперервно переходить з джерела е.р.с. в ланцюгі назад. ЇЇ значення за період =0.

Рис.

   

 (Включення конденсатора на зарядку!)

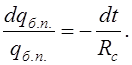
Початкова умова q(0)=0.

 

const=-e×c

Рис.

Нехай тепер: e(t)=R_eUe^iwt.

Знов комплексний метод:

q=R_eQe^iwt,

 

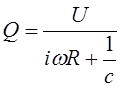
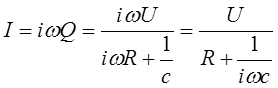
Таким чином, у ланцюгах змінного струму, окрім R виникає ще два імпеданси

X_L=iwL, та

Розглянемо тепер схему.

Рис.

Імпеданс

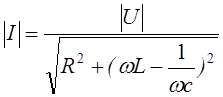
Рис.

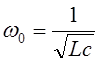 - резонансна частота Томсона. Це послідовний резонанс..