Постійний електричний струм. Теорема Остроградского-Гаусса

Лекція 5

Постійний електричний струм

при  в провіднику

При   

(кількість електронів за сек. (струм)).

 - сила струму

[I]=1 A=1 Кл/сек.

           (*) - закон збереження заряду.

Рис.

 

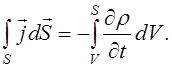
Теорема Остроградского-Гаусса:

 

 

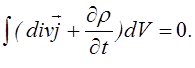
     Оскільки V  - ловільний, маємо

  - рівняння неперервності заряду.

     Розглянемо рух зарядів в електроліті

  сила тертя внаслідок в`язкості.

 

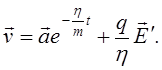
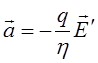     Якщо в початковий момент t=0  то  і

 

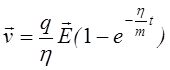
Рис.

  

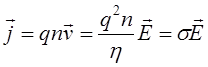
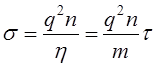
Рис.

                 

(*)

 

   

 (*)  

     (***)  

  

  

  (****)

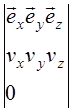
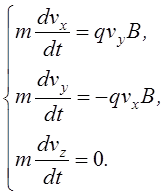
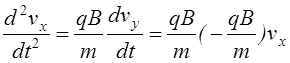
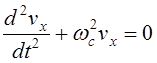
   I нехай при t=0, v_x=0.

Тоді C₁=0 і ми маємо

  

 

При цих умовах:

 

 

 

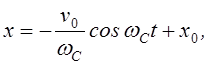
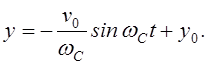
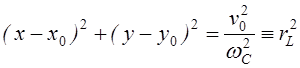
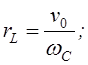
y_C – рівняння кола з радіусом;

r_L, що описано навколо точки з координатами x₀, y₀.

Рівняння

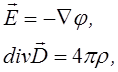
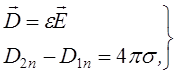      (А)

доповнені вимогою неперервності потенціалу j, представляють собою повну систему рівнянь електростатичного поля в довільному середовищі. Це значить, що якщо задані значення густини вільних зарядів r та s і значення e в кожній точці простору, і якщо на безкінечності E×R² при R®¥  залишається скінченним, то система (А) однозначно визначає електричне поле.

     Навпаки, якщо задані e та напруженість поля  (або потенціал, чи індукція) в кожній точці простору, то (А) однозначно визначає розподіл об`ємних r поверхневих s зарядів.

     Для доведення першого: припустимо, що є 2 розв’язки  і  при заданих e,r,s. Вносячи обидва рівняння в (А) і віднімаючи рівняння одне з другого, маємо

   

    

   

Значить інтеграл по всьому простору:

 

Оскільки цей  взятий по об`єму повного поля =0, то теорема доведена.