Лекція 15
Розподіл Максвелла
Візьмемо в просторі швидкостей прямокутні координатні осі, вздовж яких будемо відкладати значення vx, vу, vz окремих молекул. Тоді швидкості кожної молекули буде відповідати точка в цьому просторі. Внаслідок зіткнень положення точок будуть змінюватись (але їх густина буде залишатись незмінною – рівноважний стан).
Внаслідок рівноправності всіх напрямків руху розташування точок відносно початку координат буде сферично симетричним. Значить густина точок може залежати лише від v2. Позначимо цю густину Nf(v) ( N - повне число молекул). Тоді кількість молекул, компоненти швидкостей яких лежать у межах vx,, vx+dvx, vy,, vy+dvy, vz,, vz+dvz
Рис.
![]()
точки з швидкостями в межах v, v+dv потрапляють в кульовий шар між v та v+dv. Об’єм цієї області 4pv2dv
![]()
Розділивши на N, будемо мати ймовірність dpv того, що швидкість молекули буде в межах v, v+dv
![]()
Таким чином
![]()
Є функція розподілу молекул по модулю швидкості.
Вид функції встановив (теоретично) Максвела у 1859 р. Ось його виведення.
Ймовірність того, що vx якоїсь молекули має значення в межах vx, vx+dvx, є
![]()
Аналогічно, для двох других компонент
![]()
![]()
Оскільки всі напрямки рівноправні, то аналітичний вид функції j(vx), j(vy) j(vz) має бути однаковим.
Максвелл припустив, що ймовірність різних значень одної з компонент (vx) не залежить від величин vy, vz. Це означає, що ці події незалежні. Тому ймовірність події, що компоненти швидкості якоїсь молекули мають значення в межах vx, vy, vz; vx+dvx, vy+dvy, vz+dvz дорівнює добутку
![]()
з іншого боку
![]()
![]()
![]()
Продиф. це по vx,
![]()
![]()
![]()
![]()
![]() a - константа.
a - константа.
![]()
![]()
Аналогічно,
![]()
![]()
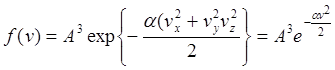
a>0 (щоб функції не зростали) A визначається з умови нормування
![]()
Обчислимо
![]()
Візьмемо
![]()
dS=dxdy
Рис.
dS-rdj×dr=r2dj
Рис.
![]()
![]()
![]()
![]()
Визначимо тепер ![]()
![]()
![]()
Таким чином, ![]()
![]()
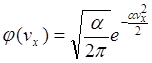
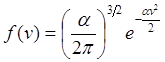
Для знаходження a, обчислимо ávx2ñ і прирівняємо отриманий
вираз знайденому з обчислень тиску ![]()
![]()
![]()
Як обчислити цей інтеграл:
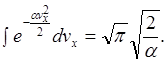
Продиференціюємо його по ![]() тоді
тоді
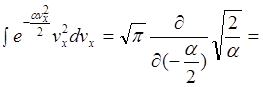
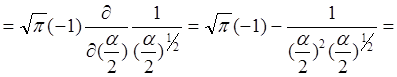
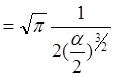
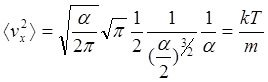
![]()
![]()
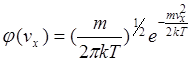
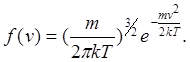
Рис.
Перше експериментальне визначення швидкостей молекул було зроблено О.Штерном у 1920 р. (через 60 років після Максвелла) Прилад складався з двох коаксіальних циліндрів.
Рис.
По осі прилада була натягнута
платинова нитка, вкрита сріблом. При нагріванні атоми срібла випаровувались.
Швидкості атомів відповідали температурі нитки. Залишивши нитку, атоми рухались
по радіусу. Внутрішній цилиндр мав вузьку поздовжну щілину, через яку проходив
назовні вузький пучок атомів. Прилад було відкачано на вакуум. Атоми срібла
залишали на поверхні зовнішнього циліндра вузьку вертикальну смужку. Якщо тепер
привести прилад у обертання, то слід зміститься на DS=wRDt, ![]()
![]()
![]()
Вимірявши w та DS, можна обчислити v.
Дослід Ламмерта (1029) і інші, підтвердили закон Максвелла.
Розподіл Больцмана (1871 р.)
Спочатку Барометрична формула
Атмосферний тиск на будь-якій висоті h обумовлений вагою шарів, що розташовані вище.
Нехай p -тиск на висоті h. Тоді на висоті h+dh буде p+dp, різниця тисків
p-(p+dp)=rgdh
dp=-rgdh.
Вважаючи газ ідеальним, маємо
p=nkT
![]()
M – середня молекулярна маса повітря
![]()
![]()
![]()
Запишемо в барометричній формулі ![]()
m – маса молекули;
k –коефіцієнт Больцмана
Замість p=nkT, а p0=n0kT
![]()
Це – розподіл молекул з висотою, який є одночасно розподілом їх за значеннями потенціальної енергії
![]()
Больцман довів, що цей розподіл справедливий не тільки для поля земного тяжіння, але й для будь-якого потенціального поля для сукупності будь-яких однакових частинок, що знаходяться у стані хаотичного теплового руху. Розподіли Максвелла і Больцмана можна об’єднати
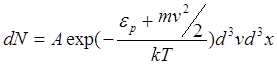
в розподіл Максвелла-Больцмана Ф.Перрен в 1909 р провів мікроскопічні спостереження розподілу броунівських частинок у поля тяжіння і визначив, що число Авогадро заключено у межах 6,6×1023 до 7,2×1023 моль. Пізніші експерименти дали 6,02×1023.
Эффективный диаметр молекулы f -минимальное расстояние, на которое сближаются при столкновении центры молекул т.к. за 1 с молекула в среднем проходит путь, равный средней арифметической скорости ávñ, и если ázñ - среднее число столкновений за 1 с, испытываемое одной молекулой, то средняя длина свободного пробега
![]()
Рис.
Найдем ázñ, пусть молекула - шарик диаметр d, которой двигается в среде других «застывших» молекул. Она сталкивается только с теми, центры которых лежат на расстоянии £d
ázñ=nV,
n – концентрация молекул,
V=pd2ávñ. Т.о.
ázñ=npd2ávñ
Если учитывать движение других молекул, то
![]()
Тогда для álñ имеем
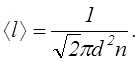
Явления переноса:
теплопроводность (перенос энергии);
диффузия (перенос массы);
внутреннее трение (перенос импульса).
Будем разбирать одномерный случай. Все явления переноса описываются законами, которые были найдены эмперически.
1. Теплопроводность подчиняется закону Фурье
![]()
jE - плотность теплового потока, т.е. энергия переносимая в форме тепла, в единицу времени через единичную площадку, перп.оси x;
l - теплопроводность;
![]() -
градиент температуры. Можно показать, что
-
градиент температуры. Можно показать, что
![]()
CV – удельная масса теплоемкости газа при постоянном объеме;
r - плотность газа.
2. Диффузия. Для химически однородного газа она подчиняется закону Фика
![]()
jm – плотность потока массы;
D – коэффициент диффузии,
![]() -
градиент плотности.
-
градиент плотности.
Можно показать, что
![]()
3. Внутреннее трение
Сила трения между двумя слоями газа (жидкости) подчиняется закону Ньютона
![]()
h - динамическая вязкость;
![]() -
градиент скорости;
-
градиент скорости;
S – площадь на которую действует сила F.
Или
![]()
jp – плотность потока импульса
![]()
Додаток
Експериментатори користуються іншими ізотермами (Амага)
Рис.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.