Е л е к т р о с т а т и к а М а г н і т о с т а т и к а
![]()
![]()
Порівняння механічних сил Fkта FA при відомих зарядах і струмах показало, що
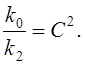
Система СІ:
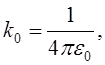
![]()
![]() Гн/м – магнітна проникність
вакууму
Гн/м – магнітна проникність
вакууму
Н а п р у ж е н і с т ь І н д у к ц і я
е л е к т р и ч н о г о п о л я м а г н і т н о г о п о л я
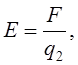
![]()
В системі СІ означення магнітної індукції
![]()
Вектор індукції B лежить в площині, ^ до провідника із струмом.
Рис.
Добуток ![]()
Напрям ![]() зв`язаний з
напрямом струму, як буравчик (правий).
зв`язаний з
напрямом струму, як буравчик (правий).
![]()
Контур не обов`язково повинен співпадати з силовою лінією. Він може бути довільним, аби тільки охоплював струм. Контур можуть пронизувати і декілька струмів I, I,…
![]() - закон повного струму.
- закон повного струму.
Приклад: поле всередині соленоїда.
Рис.
Циркуляція
всередині ![]() N- число
витків.
N- число
витків.
![]()
Якщо соленоїд тонкий, наближено
![]()
Поле всередині тонкого соленоїда не залежить від точки перерізу, тобто однорідне.
Як бути у випадку довільних струмів?
Для перетворення доведемо формулу Стокса.
![]()
S – поверхня, що спирається на контур L.
Рис.
Розглянемо
нескінченно малий контур L у площині z, y. Тоді
циркуляція ![]() дорівнюватиме
дорівнюватиме
![]()
![]()
![]()
![]()
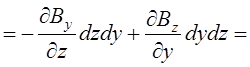
![]()
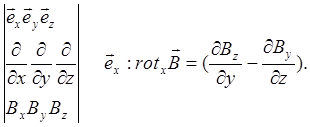
Застосуємо
тепер закон повного струму до нескінченно малого контуру, що обмежує DS в перерізі
провідника. Струм буде дорівнювати ![]() де
де
![]()
![]() - густина вільних струмів,
а
- густина вільних струмів,
а
![]() - густина зв`язаних. Тоді для
закону повного струму маємо
- густина зв`язаних. Тоді для
закону повного струму маємо
![]()
Оскільки ![]() - довільний, то мусить бути
- довільний, то мусить бути
![]() - диференціальна форма закону
повного струму.
- диференціальна форма закону
повного струму.
Експериментально відомо, що магнітних зарядів немає.
![]()
Це дає у
диференціальній формі ![]()
Таким чином, рівняння магнітостатики є
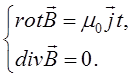
Е л е к т р о с т а т и к а М а г н і т о с т а т и к а
![]()
![]()
![]()
![]()
![]()
Додаткова
умова ![]() дає рівняння
дає рівняння
![]() (*)
(*)
![]() Аналогічно можна взяти
Аналогічно можна взяти
¯ за розв`язок (*)
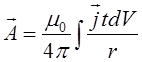
¯
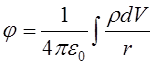
![]() - вектор-потенціал.
- вектор-потенціал.
Звернімось до обчислення вектор-потенціалу лінійного струму. Для нього
![]()
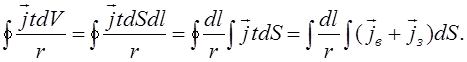
Пізніше ми покажемо, що
![]()
Тому
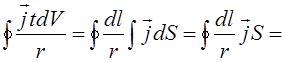
![]() - для лінійного струму
- для лінійного струму
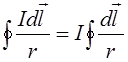
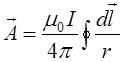
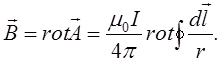
Тут виникає вираз 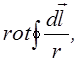 який ми обчислимо окремо.
який ми обчислимо окремо.
![]()
![]()
 Наприклад:
Наприклад:
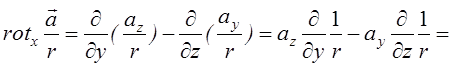
![]() Таким чином,
Таким чином,
![]() а значить
а значить
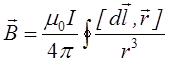 - закон Біо-Савара-Лапласа.
- закон Біо-Савара-Лапласа.
Застосуємо цей закон для визначення магнітного поля, що створене кільцевим лінійним струмом.
Рис.
![]()
![]()
![]()
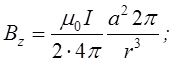
![]()
![]()
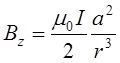
у вигляді
![]()
![]()
![]() -
вектор площини.
-
вектор площини.
Можна показати, що
поле на далеких відстанях від довільного контуру струму завжди визначається
магнітним моментом ![]()
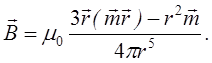
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.