Енергія електричного поля. Теорема Томсона

Лекція 3

Енергія електричного поля

Заряджаючи провідник, ми одночасно надаємо провіднику певний запас енергії.

Дійсно. Приносячи на провідник заряд dq¢, ми виконуємо роботу проти сил поля зарядів, щоФ вже є, тобто накопичуємо енергію dW=dq¢j¢. Потенціал

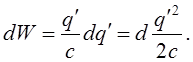
Якщо врешті заряд провідника стає q, то повна робота

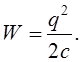
Приклад:плоский конденсатор, його ємність

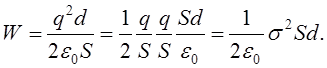
Зміст. Оскільки 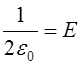 - поле однієї обкладинки. То кожна з пластин відчуває з боку іншої силу притягання

 

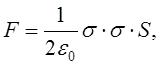
а робота

Інакше, поле всередині конденсаторає

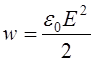  Дж/м³.

Теорема Томсона

Заряди на провіднику розташовуються так, щоб енергія електростатичного поля, що виникає, була б мінімальною.

Потенціальна енергія системи зарядів

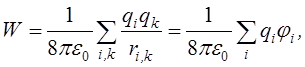
що знаходяться тільки під дією електростатичних сил, не має мінімума, чи максимума. Дійсно, до умов абсолютного ектремуму відносятся ось які: (min)

  

  

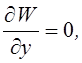
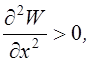
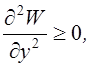
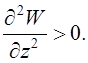
Функція  задовольняє рівнянню 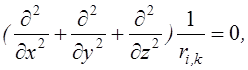 а з нею йому задовольняє і W. Значить, усі другі похідні не можуть мати однаковий знак.

Наслідок (теореми Ирншоу).

Статична конфігурація такої системи зарядів не може бути стійкою.

Електростатика діелектриків

Величина сили взаємодії двох зарядів з діелектрику (напрклад, води), що є необмеженим, складає

де  є відносна діелектрична проникність (експ.факт.). Таким чином і величина напруженості поля є:

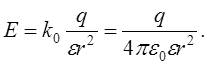
Вода: e=81, спирт: e=26 і т.д. Як і у вакуумі, електростатичне поле потенціальне, тобто  і

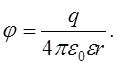
Якщо ввести вектор  (його наз. електричним зміщенням або електричною індукцією), то

Потік Y цього вектора крізь  довільну замкнену поверхню S, як і у вакуумі, дорівнює сумарному сторонньому заряду, що знаходиться всередині цієї поверхні.

В диференціальній формі

Граничні умови на межі двох діелектриків

Рис.

D_1n=D_2n, якщо на поверхні поділу нема вільних зарядів, або D_2n-D_1n=s, якщо там є вільні поверхневі заряди. Визначимо роботу по переміщенню пробного заряду вздовж цього контура.

Рис.

При внесенні плоскої пластини діелектрика в зовнішнє поле  до пластини, пластина поляризується, тобто пластина перетвориться на макроскопічний диполь з дипольним моментом

 

Застосуємо теорему Гаусса

     

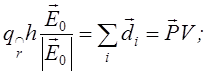
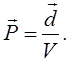
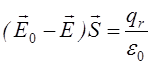
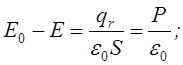
 неперервність  на межі дає

Метод електричних зображень

Рис.

Точковий заряд над нескінченною поверхнею провідника. j_q+j_q¢=0 (танг…поля).  На поверхні r=r^¢q^¢=-q. Поле у вакуумі:

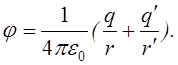
Поле в діелектрику:

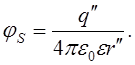
 - неперервність тангенціальної складової поля.

На межі А та В співпадають і r^¢=r^¢¢=r.

Тепер врахуємо D_1n=D_2n.

 

 

     На межі r=r^¢=r^¢¢. Крім того  Тому

 

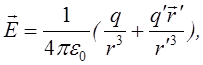
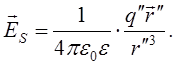
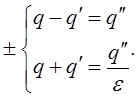
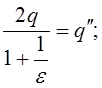
Заряд qпритягається до діелектрика

Поле диполя

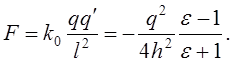
Рис.

Вектор  називають дипольним моментом

 

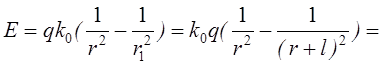
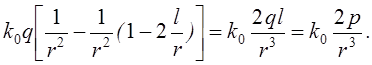
У векторній формі

Рис.

   

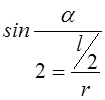
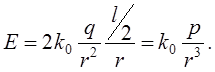
У векторній формі

Рис.

Оскільки  

 

Сила, що діє на диполь у неоднорідному полі  Для точкового диполя

 

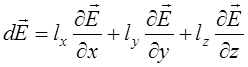
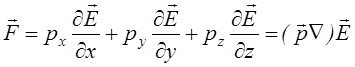
Приклад Нехай поле радіальне  (наведений диполь, оріентований по ).

Сила притягає диполь в області більш силового поля.

Конденсатори і ємність

Рис.

Поле    

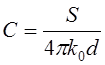   - ємність.

Таким чином 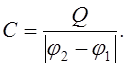 В СІ

 

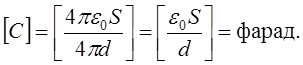
Довільну пару провідників незалежно від їх форми і розташування можна вважати конденсатором.