Тройной интеграл. Замена переменных в 3-ом интеграле. Тройной интеграл в сферических координатах

Тройной интеграл.

    Пусть задана ф-ия 3-х переменных U=¦(x;y;z) в некоторой ограниченной области Т-трехмерного пространства, тогда интеграл от этой ф-ии по области Т записывается след. образом:

Получается след. образом.

  Выполним разбиение области Т на элементарные объёмы DV₁, …, DV_n.

  Выберем в каждом элементарном объёме точку М(x_k;y_k;z_k) ®DV_k

k=1,n.

   Построим сумму вида: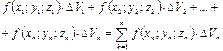

    Эта сумма называется интегральной для заданной ф-ии если существует ее придел при неограниченном увеличении числа разбиений области Т на элементарные объёмы, то он является тройным интегралом от ф-ии и записывается таким образом:

Расстановка пределов интегрирования в тройном интеграле.

   Пусть область интегрирования Т удовлетворяет след. условиям.

1.Любая прямая L ï ïOz и проходящая через область Т пересекает границу области только в двух точках:Z_вх и Z_вых.

2.Проекция тела Т на пл-ть XoY является правильной областью в направлении оси Oy (или Ox), тогда тройной интеграл в повторной записи будет выглядеть:

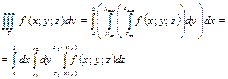
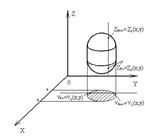
Z_вх=Z₁(x;y)

Z_вых=Z₂(x;y)       a£ x £b

Y_вх=Y₁(x;y)

Y_вых=Y₂(x;y)

Таким образом 3-й интеграл сводится к 2-у  интегрированию по проекции D.

Замечание:  Если подинтегральная ф-ия f(x;y;z) принимает только неотрицательные значения, то тройной интеграл по области Т дает нам массу тела Т т.е.

 где f(x;y;z) –плотность распределения массы по телу Т т.е. f(x;y;z)dV=dm.

Замечание: Если подинтегральная ф-ия f(x;y;z)=1, то тройной интеграл по области Т дает нам объем тела Т т.е

Пример: Вычислить тройной интеграл 

По телу Т ограниченного плоскостями : x=0;y=0;z=0;x+y+z=1

Решение.

Область Т является пирамидой

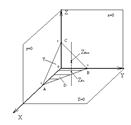
Z_ВХ: Z=0

Z_ВЫХ: X+Y+Z=1

Z_ВХ=0

Z_ВЫХ=1-X-Y

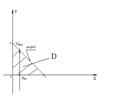
Y_ВХ=0

Y_ВЫХ=1-X

0 £ X £1

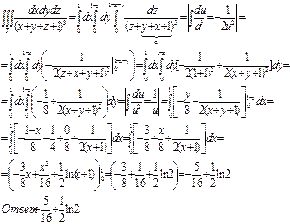
Замена переменных в 3-ом интеграле.

Пусть задана непрерывная замена: удовлетворяющая условиям:

1.) Эта замена имеет непрерывные частные производные первого порядка.

2.) Эта замена область Т в координатах  x,y,z  взаимно однозначно переводит в область Т₁ в координатах U,V,W.

3.) Якобиан перехода при этой замене сохраняет постоянный знак в области Т т.е.

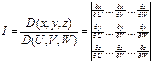
Тогда справедлива формула перехода в тройном интеграле от декартовых координат x,y,z к другим U,V,W.

Тройной интеграл в цилиндрическихкоординатах

Цилиндрическими координатами называется тройка чисел , такая что: 

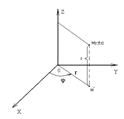
Вычислим якобиан перехода к цилиндрическим координатам.

Для этого пологаем U=r ,V=j , W=z

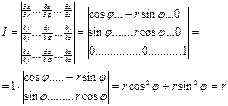
Якобиан перехода к цилиндрическим координатам совпадает с полярным радиусом: I=r, а тогда формула перехода для тройного интеграла запишется таким образом:

Заметим, то что элемент объема в цилиндрических координатах будет вычислятся по формуле:

а в дикартовых

Тройной интеграл в сферических координатах.

Тройка чисел (), называется сферическими координатами, если любая точка М в декартовых координатах связана следующими соотношениями:

Якобиан перехода при сферической замене равен:

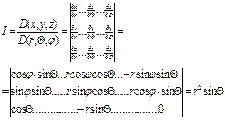
Якобиан перехода в сферических координатах имеет вид:

И тогда интеграл:

где элемент объема в сферических координатах: