Кратные интегралы. Двойные интегралы. Свойства двойного интеграла. Расстановка пределов в двойном интеграле

КРАТНЫЕ ИНТЕГРАЛЫ.

Двойные интегралы.

Для ф-ии двух переменных Z=F(x,y) можно построить интеграл вида:   где D-некоторая ограниченная область заданная на плоскости XoY.

Восполним произвольное разбиение области D на элементарные части:

В каждой элементарной площади разбиения выбираем точку с координатами (xk;yk) и вычисляем значения ф-ии в этой точке.

Затем составляем сумму вида:

которая называется интегральной суммой заданной ф-ии  Z=F(x,y) на области D.

   Если неограниченно увеличивать  число разбиений области D на элементарные площадки, то в случае существования придела интегральной суммы при  ,получаем двойной интеграл:

   Исходя из этого определения можно вычислять массу пластин объём цилиндров через двойной интеграл.

   Если задана плотность распределения массы по пластине D как ф-ия F(x,y)>=0, то масса пластины:

Если задано тело вида

Если облать D задана в декартовых координатах, то элемент площади dS будет вычисляться по ф-ле:

И тогда двойной интеграл в декартовых координатах:

Свойства двойного интеграла.

1.

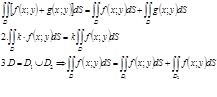
4.Для двойного интеграла справедлива следующая оценка:

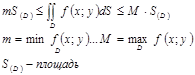
5. Для двойного интеграла справедлива теорема о среднем значении ф-ии, т.е. существует некоторая точка что значение ф-ии в этой точке находится как отношение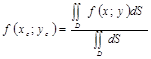

где двойной интеграл:дает нам площадь области D, т.е.

Расстановка пределов в двойном интеграле.

1.Интеграл по прямоугольной области.

Прямоугольная область D задаётся неравенствами:

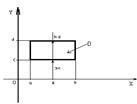
И тогда двойной интеграл по области D:

2. Если область D является правильной в направлении оси Oy, т.е. в вертикальном направлении имеет только одну точку выхода и одну точку входа, то она (область) задается неравенствами:

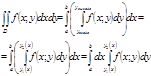
3. Если область D является правильной в направлении оси Ox, т.е. имеет вид:

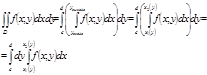
Замечание: Если область D не является правильной, то вертикальными или горизонтальными прямыми разбиваем ее на правильные части, и затем интегрируем по каждой получившейся части.