Углы между прямыми и плоскостями. Векторы в пространстве: Вариативные тестовые вопросы по геометрии (Варианты 1-4 по 12 вопросов с отметками правильных ответов)

Геометрия 10 класс. Тема: Углы между прямыми и плоскостями. Векторы в пространстве

Цель данного теста — проверить, умеет ли учащийся:

¾  решать задачи на нахождение угла между прямой и плоскостью; между двумя скрещивающимися прямыми; между плоскостями;

¾  находить сумму, разность векторов, произведение вектора на число, скалярное произведение векторов;

¾  применять векторы к решению задач.

Вариант 1

1. Из точки S проведен перпендикуляр SA и наклонные SB и SC к плоскости a. Выберите правильное утверждение. –А. Проекцией прямой SB на плоскость a является прямая BC . –Б. Углом между прямой SB и ее проекцией на плоскость a является угол SBC.

+В. Углом между прямой SB и плоскостью a является угол SBA.

–Г. Углом между прямой SB и плоскостью a является угол BSA.

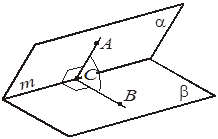
–А. Плоскость ABC не перпендикулярна прямой m.

–Б. Углом между плоскостями a и b является угол между прямыми AC и m.

+В. Угол между плоскостями a и b равен 60°.

–Г. Плоскости a и b перпендикулярны.

3. В пространстве даны точки A(–1; 0; 3), B(–1; 1; 0). Выберите правильное утверждение. –А. Вектор имеет координаты (–1; 1; 3). –Б. Вектор имеет координаты (–1; 0; 3). +В. < . –Г. = .

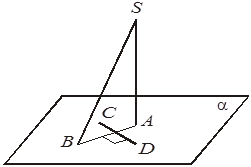
+А. Прямая AB является проекцией прямой SB на плоскость a.

–А. Прямая CD является проекцией прямой SB на плоскость a.

+Б. Прямая CD перпендикулярна плоскости SAB.

–Б. Прямая CD не перпендикулярна плоскости SAB.

+В. Прямые SB и CD перпендикулярны.

–В. Прямые SB и AB перпендикулярны.

+Г. Угол между прямыми SA и CD равен 90°.

–Г. Угол между прямыми SA и CD не равен 90°.

5. В кубе ABCDA1B1C1D1 проведено сечение плоскостью, которая проходит через точки A1, D, C. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. +А. Плоскость ADD1 перпендикулярна линии пересечения секущей плоскости и плоскости ABC. –А. Плоскость ABB1 перпендикулярна линии пересечения секущей плоскости и плоскости ABC.

+Б. Угол между секущей плоскостью и плоскостью ABC — это угол между прямыми AD и DA₁.

–Б. Угол между секущей плоскостью и плоскостью ABC — это угол между прямыми AD и DC.

+В. Угол между секущей плоскостью и плоскостью ABC равен углу ADA₁.

–В. Угол между секущей плоскостью и плоскостью ABC равен углу BDB₁.

+Г. Угол между секущей плоскостью и плоскостью ABC равен 45°.

–Г. Угол между секущей плоскостью и плоскостью ABC равен 60°.

+А. Вектор (–1; –1; 0) — противоположный вектору .

–А. Вектор (0; –1; –1) — противоположный вектору .

+Б. Длина вектора равна .

–Б. Длина вектора равна 1.

+В. Вектор 2 + имеет координаты (2; 3; 1).

–В. Вектор 2 + имеет координаты (2; 2; 2).

+Г. Длины векторов и  равны.

–Г. Длины векторов и  не равны.

+А. Прямая BD является проекцией прямой BD₁ на плоскость ABC .

–А. Прямая AC является проекцией прямой BD₁ на плоскость ABC .

+Б. Прямая BD₁ перпендикулярна прямой AC.

–Б. Прямая BD₁ не перпендикулярна прямой AC.

+В. Прямая AC перпендикулярна плоскости DBB₁.

–В. Прямая AC перпендикулярна плоскости BD₁C₁.

+Г. Прямая BD₁ наклонена к плоскости ABC под углом .

–Г. Прямая BD₁ наклонена к плоскости ABC под углом .

+А. Угол между плоскостями ABC и a равен  углу CMO, где M — середина стороны AB.

–А. Угол между плоскостями ABC и a равен  углу MCB, где M — середина стороны AB.

+Б. Длина перпендикуляра CO равна 4 см.

–Б. Длина перпендикуляра CO равна 3 см.

+В. Треугольник AOB является ортогональной проекцией треугольника ABC на плоскость a.

–В. Треугольник ABC является ортогональной проекцией треугольника