Планиметрия: Пособие по геометрии для подготовительных курсов (Треугольник. Окружность и круг. Элементы аналитической геометрии. Задачи на отыскание геометрических фигур с экстремальными значениями элементов)

A. Построение отрезков по формулам, представляющим собой сумму, разность (x = a ± b), а также умножение либо деление на число (x = ka или x = —), сводится к сложению или вычитанию отрезков, k

увеличению отрезка в заданное число раз и делению отрезка на заданное число равных частей.

I  2       2       /2 2

Б. Построение отрезков по формулам x = \]a + b , x = \]a - b сводится к построению прямоугольного треугольника по его катетам, либо гипотенузе и катету. В первом случае x — гипотенуза, во втором -катет.

ab a²

B.       Построение отрезков по формулам x = — или x = — сводится

c c

к нахождению четвертого пропорционального отрезка. Для этого используется теорема о пересечении сторон угла параллельными прямыми (см. рис. 23 этой главы).

a² г~г Г. Построение отрезков по формулам x = — или x = V ab удобно

c

выполнять, используя теорему о перпендикуляре, опущенном из произвольной точки окружности на диаметр.

На рисунках 22 и 23 показано, как строить отрезок, выраженный последними двумя формулами.

Рис. 22

Д. Построение отрезков по формулам, представляющим комбинации приведенных выше формул, выполняется путем введения вспомогательных неизвестных отрезков и последовательного их отыскания.

В частности, для формул имеющих сложный вид, их можно представить в виде суперпозиции перечисленных выше формул. Например,

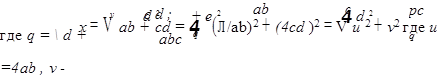a

отрезок x невозможно, если не задан единичный отрезок.

Если единичный отрезок задан, то построение осуществляется просто:

_a2

a ■ a

1    i ■ 1    Г I—л

— =   , va = Va ■ 1 .

Примеры.

(a + b)(b — c)

1.Построить отрезок, выраженный формулой x =         .

a+c

Решение. □ Для построения x последовательно строим четыре отрезка:

yz

y = a + b,   z = b — c,   t = a + c,   x = —. ❖

2.Построить отрезок, выраженный формулой

a²+ 2ab+ b²

x =      .

a+c

Решение. □ Преобразовав заданную формулу к виду

= a²+ 2ab + b² = (a + b)²

a+c a+c _y2

строим отрезки y = a + b, z = a + c . Тогда x = ^— . ❖

z

Замечание. Без преобразования после почленного деления в исходной формуле пришлось бы выполнить пять операций.

ab^a ² + b ²

3.----------------------------------------------- Построить отрезок, выраженный формулой x =---------------------- .

cd

ab                                        _{2     2} yz

Решение. □ Положим y = —,   z = л1 a  + b   . Тогда x = — . ❖

cd

4.       Построить отрезок, выраженный формулой

y = 4a² + b² и z = >Jc² — d² . Тогда x = 4y² + z² . ♦

Замечание. В этом примере, как и во многих других, вводя новые отрезки, можно подбирать разные комбинации заданных. Наилучшим решением будет такое, которое требует минимального количества операций.

4/   4     i 4

5. Построить отрезок, выраженный формулой x = \ a  + b Решение. □ Выполним преобразования

x = ⁴ a ⁴ + b ⁴

' b ² >

v ^a J

b

Обозначим у = —, z = у a

22

+ у ,тогда x =

4az . ♦

6. В данный треугольник ABC вписать квадрат MQPN так, чтобы две его вершины Q и P лежали на основании BC , а две другие - на боковых сторонах.

Решение. □ Эта задача уже была решена методом подобия (задача №2 настоящей главы).

Строим высоту AD треугольника ABC. Обозначим BC = a , AD = h, MN = MQ = x (см. рис. 24).

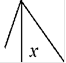
Ml fx

A

h

N

Так как треугольник ABC задан, то отрезки BC= a и AD = h известны. Выразим длину отрезка x по формуле через длины отрезков a и h .

Из подобия треугольников ABC и AMN (в них по условию jMN || BC)

h

B Q D ^a P

Рис. 24

C

находим — =

x

h - x

x=

откуда

ah

a+h

Построив по выведенной формуле сторону x квадрата MQPN , проводим на расстоянии x от основания BC прямую jMN || BC. Получив точки M и N, опустим MQ A BC и NP A BC .

Искомый квадрат MNPQ построен (см. рис. 24). ❖

Глава 3. Треугольник

§ 1. Основные определения

Треугольником называется фигура, образованная замкнутой ломаной, состоящей из трех звеньев, т.е. треугольник - это n-угольник при n = 3.

Для краткости слово треугольник обозначается символом л . Вершины треугольника обычно обозначают большими буквами латинского алфавита, а противоположные им стороны теми же малыми буквами. Например, вершины A, B и C , а противоположные им стороны a, b, c .

Если все три угла треугольника острые, то он называется остроугольным, а если один из его углов тупой, то - тупоугольным. Треугольник, имеющий прямой угол, называется прямоугольным.

Теорема. (Определение вида треугольника по его сторонам). Пусть a, b и c - стороны треугольника, причем c - наибольшая сторона; тогда:

2        2 2

а)       если c < a + b , то треугольник остроугольный;

б)       если c ² = a ² + b ², то треугольник прямоугольный;

2       2 2

в)       если c > a + b , то треугольник тупоугольный.

Углы треугольника не могут быть заданы произвольно, поскольку имеет место теорема.

Теорема. Во всяком треугольнике сумма углов равна 180° или п радиан