Многоугольники. Длина окружности: Вариативные тестовые вопросы по геометрии (Варианты 1-4 по 12 вопросов с отметками правильных ответов)

Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. BP = PC.

–А. BP > PC.

+Б. ÐCBP= 60°.

–Б. ÐCBP = 90°.

+В. Длина дуги PC равна .

–В. Длина дуги PC равна .

+Г. Длина дуги AP равна  длины дуги BP.

–Г. Длина дуги AP равна  длины дуги BP.

4-й уровень

10. Сторона квадрата ABCD равна 2a; O — точка пересечения его диагоналей. Окружность с центром O пересекает стороны квадрата в точках A₁, A₂, B₁, B₂, C₁, C₂, D₁, D_2. Известно, что BB₁ = (2 –) a. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

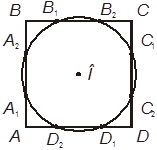
+А. Периметр треугольника BB₁A₂ равен 2a.

–А. Периметр треугольника BB₁A₂ равен a.

+Б. A₂B_1 = B₁B₂.

–Б. A₂B₁ > B₁B₂.

+В. ÐA₂B₁B₂= 135°.

–В. ÐA₂B₁B₂ = 150°.

+Г. 8-угольник A₁A₂B₁B₂C₁C₂D₁D₂ правильный.

–Г. 8-угольник A₁A₂B₁B₂C₁C₂D₁D₂ не является правильным.

11. Правильный 8-угольник со стороной a вписан в окружность (см. рисунок). Радиус окружности обозначим R. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. .

–А. .

+Б. .

–Б. .

+В. .

–В. .

+Г. .

–Г. .

12. Три равные окружности, лежащие вне окружности радиуса r, касаются между собою и касаются данной окружности (см. рисунок). Обозначим центры больших окружностей A, B и C, а радиусы этих окружностей — R. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

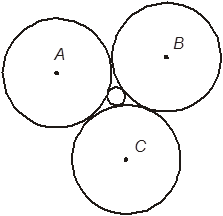
+А. Высота треугольника ABC равна.

–А. Высота треугольника ABC равна .

+Б. Радиус окружности, описанной около треугольника ABC, равен .

–Б. Радиус окружности, описанной около треугольника ABC, равен .

+В. .

–В. .

+Г. Длина меньшей окружности относится к длине большей окружности как.

–Г. Длина меньшей окружности относится к длине большей окружности как .

Вариант 3

Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите . Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным.

1-й уровень

1. На рисунке изображена ломаная PQRS. Выберите правильное утверждение. +А. PR<PQ+ QR. –Б. PQ+ QR+ RS = PS. –В. Длина ломаной PQRS меньше PS. –Г. Длина ломаной QRS меньше QS.

2. На рисунке изображены квадрат и окружность. Выберите правильное утверждение. –А. Квадрат вписан в окружность. –Б. Окружность описана около квадрата. +В. Окружность вписана в квадрат. –Г. Радиус окружности равен стороне квадрата.

3. Точки A, B и C лежат на окружности с центром O (см. рисунок). Известно, что OA = 2 см, ÐCOB = 30°, ÐBOA = 90°. Выберите правильное утверждение. –А. Радианная мера угла AOB равна . +Б. Радианная мера угла AOC равна . –В. Длина дуги BC равна  длины окружности. –Г. Длина окружности равна 2p см.

2-й уровень

4. ABCD — выпуклый четырехугольник. Известно, что ÐA + ÐB = 270°. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. ÐC + ÐD = 90°.

–А. ÐC + ÐD = 180°.

+Б. Угол D острый.

–Б. Угол D может быть тупым.

+В. BD² < BC² + CD².

–В. BD² > BC² + CD².

+Г. BD² > AB² + AD².

–Г. BD² < AB² + AD².

5. Около правильного треугольника описана окружность, и в этот же треугольник вписана окружность (см. рисунок). Обозначим радиус вписанной окружности r, а радиус описанной окружности — R. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. R= 2r.

–А. R= 3r.

+Б. Центр описанной окружности совпадает с точкой пересечения медиан треугольника.

–Б. Центр вписанной окружности не совпадает с точкой пересечения медиан треугольника.

+В. Сторона треугольника равна .

–В. Сторона треугольника равна .

+Г. Сторона треугольника равна .

–Г. Сторона треугольника равна .

6. Две окружности с центрами в точках O₁ и O₂ пересекаются в точках A и B, причем первая окружность проходит через центр второй окружности. Радиус каждой окружности равен 10 см. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. Расстояние между центрами окружностей равно 10 см.

–А. Расстояние между центрами окружностей равно 20 см.

+Б. Четырехугольник AO₁BO₂ — ромб с углами 60° и 120°.

–Б. Четырехугольник AO₁BO₂ — ромб с углами 30° и 150°.

+В. Длина каждой окружности равна 20p см.

–В. Длина каждой окружности равна 10p см.

+Г. Длина дуги AO₁B равна  см.

–Г. Длина дуги AO₁B равна  см.

3-й уровень

7. Дуга BC окружности с центром A соответствует центральному углу 120°. Вторая окружность с центром O касается отрезков AB и AC и дуги BC. Радиусы окружностей обозначим R и r (R> r). Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. ÐCAO = 60°.

–А. ÐBAO < 60°.

+Б. .

–Б. .

+В. .

–В. .

+Г. Отношение длины окружности с центром O к длине дуги BC равно .

–Г. Отношение длины окружности с центром O к длине дуги BC равно .

8. Около окружности с центром O и радиусом r описана равнобокая