Преобразования фигур на плоскости. Векторы: Вариативные тестовые вопросы по геометрии (Варианты 1-4 по 12 вопросов с отметками правильных ответов)

Тест 10. Тема: Преобразования фигур на плоскости. Векторы

Цель данного теста — проверить, умеет ли учащийся:

¾  выражать координаты вектора через координаты его начала и конца;

¾  вычислять длину вектора;

¾  выполнять операции над векторами;

¾  находить скалярное произведение векторов и угол между векторами;

¾  применять векторы при решении геометрических задач;

¾  использовать определение и свойства центральной и осевой симметрии; находить фигуры, имеющие симметрию.

Вариант 1

Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите . Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным.

1-й уровень

1. На рисунке изображен квадрат ABCD. Выберите правильное утверждение. –А. Точка A является центром  симметрии квадрата ABCD. –Б. Точка B является центром  симметрии квадрата ABCD. +В. Прямая AC является осью симметрии квадрата ABCD. –Г. Прямая AB является осью симметрии квадрата ABCD.

2. Даны точки O(0; 0), A(–4; –2) и вектор (a₁; a₂). Зная, что координатами вектора называются числа a_1 = x₂ – x₁, и a₂ = y₂ – y₁, где (x₁; y₁) — координаты начала вектора, (x₂; y₂) — координаты конца вектора, выберите правильное утверждение.

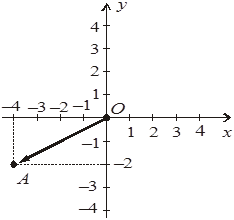
+А. a₂ = –2-0.

–Б. a₁ = 0–(–4).

–В. a₁ > 0.

–Г.  =  .

3. Даны параллелограмм ABCD и векторы и . Выберите правильное утверждение. –А. Модуль вектора больше отрезка AB. –Б. Вектор не равен вектору . +В. Модули векторов  и равны. –Г. Векторы  и направлены противоположно.

2-й уровень

4. Дан остроугольный треугольник ABC. Преобразование симметрии относительно точки C переводит точку A в точку A₁, а точку B — в точку B_1. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. AC = CA₁.

–А. AC = 2CA₁.

+Б. Прямые AB и A₁B₁параллельны.

–Б. Прямые AB и AB₁ параллельны.

+В. Треугольники ABC и A₁B₁C равны.

–В. Треугольники ABC и A₁B₁A равны.

+Г. Четырехугольник ABA₁B₁ — параллелограмм.

–Г. Четырехугольник ABA₁B₁ — квадрат.

5. Даны векторы (–2; 5) и (6; –2). Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. ½ ½=.

–А. ½ ½= .

+Б. + = .

–Б. + = .

+В. – = .

–В. – = .

–Г. ½ – ½= 5.

+Г. ½ + ½= 5.

6. Дан параллелограмм ABCD, = , = . Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. + = .

–А. + =.

+Б. + =.

–Б. + = .

–В. + = .

+В. + =.

+Г. = –.

–Г. = .

3-й уровень

7. Фигура состоит из двух касающихся окружностей одинакового радиуса. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. Точка касания окуружностей является центром симметрии данной фигуры.

–А. Центр одной из окружностей является центром симметрии данной фигуры.

+Б. Любая ось симметрии данной фигуры проходит через точку касания окружностей.

–Б. Данная фигура имеет только одну ось симметрии.

+В. Данная фигура имеет две оси симметрии.

–В. Данная фигура имеет три оси симметрии.

+Г. Данная фигура имеет центр симметрии.

–Г. Данная фигура имеет два центра симметрии.

8. Вершинами параллелограмма ABCD являются точки A(1; –3), B(4; 2), C(–3; 2), D(x_D; y_D). Диагонали параллелограмма пересекаются в точке O. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. = .

–А. = .

+Б. x_B – x_A = x_C – x_D.

–Б. x_B – x_A = x_D – x_C .

+В. Точка D имеет координаты: x_D = –6; y_D = –3.

–В. Точка D имеет координаты: x_D = 0; y_D = 4.

+Г. = .

–Г. = .

9. В треугольнике ABC отрезки AN и CM — медианы, O — точка пересечения медиан. Зная, что медианы точкой O делятся в отношении 2:1, считая от вершины, отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. .

–А. .

+Б. .

–Б. .

+В. .

–В. .

+Г. .

–Г. .

4-й уровень

10. BK — высота треугольника ABC. Известно, что , . Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. Вектор ( – ) перпендикулярен вектору .

–А. Вектор ( + ) перпендикулярен вектору .

+Б. = .

–Б. = .

+В. .

–В. .

+Г. .

–Г. .

11. Начала векторов  и  совпадают. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. Модуль вектора  равен 1.

–А. Модуль вектора  больше 1.

+Б. Векторы  и  направлены одинаково.

–Б. Векторы  и  направлены противоположно.

+В. Модули векторов  и  равны.

–В. Модули векторов  и  не равны.

+Г. Вектор = + делит пополам угол между векторами  и .

–Г. Вектор = – делит пополам угол между векторами  и .

12. В треугольнике ABC точка K лежит на стороне BC, причем CK : KB = 9:1. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

+А. .

–А. .

+Б. .

–Б. .

+В. .

–В. .

+Г. .

–Г. .

Вариант 2

Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите . Если хотя бы одна буква из 4-х будет не отмечена, задание считается невыполненным.

1-й уровень

1. На рисунке изображен равносторонний треугольник ABC. Выберите правильное утверждение. –А. Точка A является центром симметрии треугольника ABC. –Б. Треугольник ABC имеет центр симметрии.

–В. Прямая, проходящая через середины отрезков AC и AB, является осью симметрии треугольника ABC.

+Г. Треугольник ABC имеет ось симметрии.

2. Даны точки O(0; 0), B(3; –2) и вектор (a₁; a₂). Зная, что координатами вектора называются числа a_1 = x₂ – x₁, и a₂ = y₂ – y₁, где (x₁; y₁) — координаты начала вектора, (x₂; y₂) — координаты конца вектора, выберите правильное утверждение.

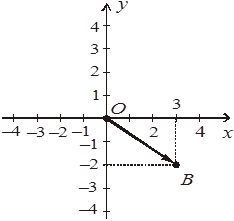
–А. a₁ = 0-3.

–Б. a₂ = 0–(–2).

+В. a₁ > 0.

–Г.  =  .

3. Дана трапеция ABCD и векторы и . Выберите правильное утверждение. +А. Векторы  и  коллинеарны. –Б. Модули векторов  и равны. –В. Вектор  равен вектору . –Г. Векторы и  противоположны.

2-й уровень

4. Точки A и B лежат по одну сторону от прямой m. Преобразование симметрии относительно прямой m переводит точку