
29.10.98.
y=f(x) (-p;p)
![]()
![]()
![]()
![]()
Пример!
Задана функция ![]() представить его тригонометрическим рядом Фурье.
представить его тригонометрическим рядом Фурье.
Решение!
Построим график функции на отрезке [-p;p], и периодически его продолжим на всю числовую ось.
По формулам находим коэффициенты Фурье для этой функции:
![]()
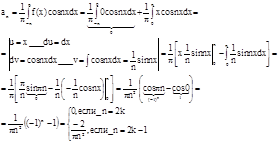 Аналогично вычисляем коэффициент bn:
Аналогично вычисляем коэффициент bn: ![]()
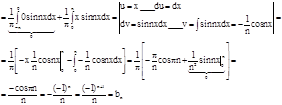 Искомый
ряд Фурье для заданной функции имеет вид:
Искомый
ряд Фурье для заданной функции имеет вид:
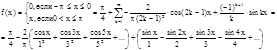 Ряды
Фурье для четной и нечетной функций.
Ряды
Фурье для четной и нечетной функций.
а)Интеграл
от нечетной функции по симметричному промежутку равен нулю т.е.: ![]() ,
если f(-x)= -f(x)
,
если f(-x)= -f(x) 
Например: f(x)=x; f(x)=x3; f(x)=sinx; f(x)=x cosx.
б)Интеграл от четной функции
по симметричному промежутку равен удвоенному интегралу по половине промежутка,
т.е.: ![]() , если f(-x)=f(x)
, если f(-x)=f(x) 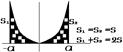
Например: f(x)=x2; f(x)=cosx; f(x)=x sinx.
Для четных и нечетных функций выполняются свойства:
1)Чёт*Чёт=Чет
2)Нечет*Чет=Нечет
3)Нечет*Нечет=Чет
Например:![]()
![]()
Поэтому,
для четной функции разложение в ряд Фурье идет только по косинусам: ![]() (1), где
(1), где 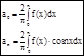 (2)
(2)
f(-x)=f(x), действительно 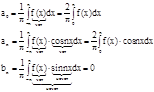
Аналогично
для нечетной функции разложение в ряд Фурье пойдет только по синусам: ![]() (3), где
(3), где ![]() (4),
(4), ![]()
Действительно: 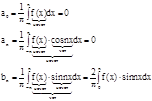
Пример! (для четной функции)
Разложить в ряд Фурье функцию: ![]() [-p;p]
[-p;p]
Решение!
Нарисуем график функции на промежутке от -p до p и периодически его продолжим: ![]()
Раскладываем в ряд Фурье: т.к. функция f(x) является нечетной ее график симметричен относительно начала координат: f(-x)=-f(x), поэтому разложение в ряд Фурье идет только по синусам, значит: a0=0 ; an=0 , при n=1,¥
Вычисляем коэффициенты bn по формуле:
![]()
![]()
Выписываем ряд Фурье: ![]()
![]()
Пример! (для четной функции)
Разложить
в ряд Фурье функцию f(x)=x2
на промежутке [-p;p], и с помощью полученного разложения показать, что: ![]() и
и ![]()
Решение: ![]()
Заметим, что график симметричен относительно оси ординат, т.е. функция четная f(-x)=f(x), и тогда разложение в ряд Фурье идет только по косинусам, где bn=0.
Находим ![]()
Находим аn:
![]()
![]()
![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.