Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Прямая SO перпендикулярна плоскости АСВ.
+Б. ЕслиSA =
см, АВ =см, то SO = 1 см.
+В. Прямая BD перпендикулярна плоскости АСS.
–Г. Прямая BD перпендикулярна плоскости SCD.
8. Из точки А к плоскости a проведен перпендикуляр ABи наклонные AC и AD. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Если AD =
см, AC =
см, AB =
см, то BD – BC = 1 см.
+Б. Если AD =см, AC =см, то BD > BC.
+В. Если AC = 2 см,
ÐACB = 60°, AD =
см, то BD = 2
см.
–Г. Если AD = AC, ÐDAC = 60° и АВ = BС, то ÐDВС > 90°.
9. Точка K равноудаленна от вершин равнобедренного треугольника ABC, KO — перпендикуляр к плоскости ABC, расстояние от точки Kдо плоскости ABC равно 1 см. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
–А. Точка O обязательно является центром окружности, вписанной в треугольник ABC.
+Б. Точка O обязательно является центром окружности, описанной около треугольника ABC.
–В. Середина отрезка KA находится на расстоянии 1 см от плоскости ABC.
+Г. Если M, L, N — середины отрезков KA, KB, KC, то расстояние между плоскостями ABC и MLN равно 0,5 см.
10. Дан прямоугольный параллелепипед ABCDA1B1C1D1, в котором AB = a, BС = b, CC1 = c (a < b < c). Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
–А. Треугольник ABC1 может быть тупоугольным.
–Б. Треугольник ABC1 может быть равнобедренным.
+В. ОтрезкиAC1 и ВD1 пересекаются в точке, которая является серединой каждого из них.
+Г. Величина угла C1AB равна arctg 
.
11. В пирамиде SАВС ребра SA, SB, SC попарно перпендикулярны и SA = SB = SC = a. Из точки S на плоскость АВС проведен перпендикуляр SO. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Точка O является точкой пересечения медиан треугольника ABC.
–Б. Длина перпендикуляра SO равна 
.
+В. Прямая SC перпендикулярна плоскости АВS.
+Г. Плоскость, которая проходит через ребро AS и перпендикулярна СВ, проходит через середину ребра CB.
12. Через вершину B параллелограмма ABCD проведена плоскость на расстоянии 5 см от диагонали AC, точки K и M — середины отрезков AD и DC. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Прямая AC параллельна проведенной плоскости.
–Б. Точка D находится на расстоянии 5 см от проведенной плоскости.
+В. Прямая KM параллельна проведенной плоскости.
–Г. Расстояние от прямой KM до построенной плоскости равно 5 см.
Вариант 2
Записывая ответы на
задания теста, обведите буквы, отвечающие утверждениям,
которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям,
которые вы считаете неправильными. Например, если вы считаете правильными
утверждения А и В, а неправильными — утверждения Б и Г, запишите 
. Если хотя бы одна буква из 4-х будет не
отмечена, задание считается невыполненным.
1. Точка S лежит вне плоскости треугольника ABC, причем SA^AC и AB ^AC, SA = AB = SB . Выберите правильное утверждение.
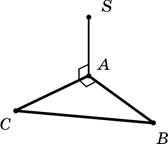
–А. Прямая SA перпендикулярна плоскости ABC.
–Б. Прямая AB перпендикулярна плоскости SAC.
+В. Прямая AC перпендикулярна плоскости SAB.
–Г. Прямая BC перпендикулярна плоскости ASC.
2. Из точки A к плоскости a проведен перпендикуляр AB и наклонные AC и AD. Выберите правильное утверждение.
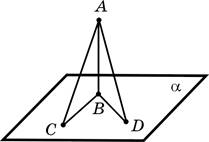
–А. Прямая AD перпендикулярна плоскости a.
–Б. Прямая AD перпендикулярна прямой BD.
–В. Если AD = АС, то BD < ВС.
+Г. Среди отрезков AC, AB, AD наименьшим является AB.
3. ABCDA1B1C1D1 — куб, ребро которого равно 1 см. Выберите правильное утверждение.
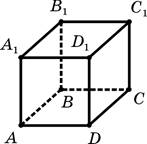
–А. Расстояние от точки A до плоскости BCC1 меньше 1 см.
–Б. Расстояние от точки C до точки A равно 2 см.
+В. Расстояние от прямой А1B1 до плоскости ABC равно 1 см.
–Г. Расстояние между плоскостями ABB1 и DCC1больше 1 см.
4. Дана плоскость a, параллельная ей прямая a и некоторая прямая b, которая не лежит в плоскости a. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Если b || a, то b обязательно параллельна a.
–Б. Если b ^ a, то b обязательно перпендикулярна a.
+В. Если b ^a и b пересекает a, то b ^ a.
–Г. Если b ^a, то b и a обязательно скрещивающиеся.
5. Через центр О квадрата ABCD проведен перпендикуляр SO к плоскости ABC. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Расстояния SA, SB, SC, SD равны.
+Б. Угол SDO равен углу SAO.
–В. Если OA = см, SС = см, то SO = 2 см
–Г. Если SA = 2OA, то ÐOSA = 45°.
6. Отрезок AB, длина которого 13 см, не пересекает плоскость a, точка С — середина отрезка AB. Расстояния от точек Aи B до плоскости a равны
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
