рисунке окружности с центрами в точках A и B касаются друг друга в точке K и касаются окружности с центром O, радиус которой равен R. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
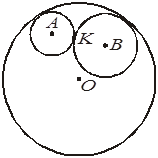
+А. Точка K лежит на прямой AB.
–А. Точка K не лежит на прямой AB.
+Б. OA + AK = R.
–Б. OA + AK < R.
+В. OA + AK = OB + BK.
–В. OA + AK < OB + BK.
+Г. Периметр треугольника OAB равен 2R.
–Г. Периметр треугольника OAB равен 3R.
11. Точки A, B и C лежат на окружности с центром O; AB — диаметр окружности. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. ÐACB = 180° – (ÐABC + ÐBAC).
–А. ÐACB = 180° – ![]() .
.
+Б. ![]() .
.
–Б. ÐABC + ÐBAC = ÐAOC + ÐBOC.
+В. ÐAOC + ÐBOC = 180°.
–В. ÐAOC + ÐBOC = 200°.
+Г. ÐACB = 90°.
–Г. ÐACB = 100°.
12. Дана окружность с центром O. Диаметр CD пересекает хорду AB в точке K, которая является серединой радиуса OD и хорды AB. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Отрезок AK является одновременно медианой и высотой треугольника OAD.
–А. Высота и медиана треугольника OAD, проведенные из вершины A, не совпадают.
+Б. Треугольник OAD равносторонний.
–Б. Треугольник OAD прямоугольный.
+В. ÐACO = 30°.
–В. ÐACO = 45°.
+Г. Треугольник ABC равносторонний.
–Г. Отрезок AB может быть длиннее отрезка AC.
Вариант 2
Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям,
которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям,
которые вы считаете неправильными. Например, если вы считаете правильными
утверждения А
и В, а неправильными — утверждения Б и Г, запишите ![]()
![]()
![]()
![]() . Если хотя бы одна буква из
4-х будет не отмечена, задание
считается невыполненным.
. Если хотя бы одна буква из
4-х будет не отмечена, задание
считается невыполненным.
1-й уровень
|
1. На рисунке изображена окружность с центром O. Известно, что радиус окружности равен 10 см. Выберите правильное утверждение. –А. Отрезок AB — радиус окружности. –Б. Отрезок CO — диаметр окружности. –В. OC = 5 см. +Г. AB = 20 см. |
|
|
2. Точка A лежит на окружности с центром O. Прямая a проходит через точку A и перпендикулярна радиусу OA. Выберите правильное утверждение. –А. Один из углов, образованных при пересечении прямых a и OA, острый. +Б. Прямая a является касательной к окружности. –В. Через точку A можно провести две касательные к данной окружности. –Г. Расстояние от точки O до прямой a больше радиуса окружности. |
|
|
3. На рисунке изображена окружность и треугольник ABC. Выберите правильное утверждение. –А. Окружность вписана в треугольник ABC. –Б. Окружность описана около треугольника ABC. +В. Отрезок AB — хорда окружности. –Г. Прямая AB — касательная к окружности. |
|
2-й уровень
|
4. Дана окружность с центром O. Хорда AB не проходит через центр окружности и пересекает диаметр CD в точке K. Известно, что AK = KB. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. +А. Треугольник AOB обязательно равнобедренный. –А. Треугольник AOB обязательно равносторонний. +Б. Отрезок OK — медиана треугольника AOB. –Б. OK > OB. +В. Высота и медиана треугольника AOB, проведенные из вершины O, совпадают. –В. Высота и медиана треугольника AOB, проведенные из вершины O, не совпадают. +Г. Диаметр CD перпендикулярен хорде AB. –Г. Один из углов, образованных при пересечении прямых AB и CD, острый. |
|
5. Две окружности с центрами O1 и O2 и радиусами r1 и r2 (r1> r2) пересекаются в точках A и B. Отрезки AB и O1O2 пересекаются в точке K. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Треугольник O1AO2 неравнобедренный.
–А. Треугольник O1AO2 равнобедренный.
+Б. Отрезок AK — высота треугольника O1AO2.
–Б. Отрезок AK — медиана треугольника O1AO2.
+В. Середина отрезка O1O2 не лежит на прямой AB.
–В. Середина отрезка O1O2 лежит на прямой AB.
+Г. Середина отрезка AB лежит на прямой O1O2.
–Г. Середина отрезка AB не лежит на прямой O1O2.
6. Дан треугольник ABC. Точка O лежит на серединном перпендикуляре к отрезку AB. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. AO = OB.
–А. AO ¹ OB.
+Б. Если окружность с центром O проходит через точку A, то она обязательно проходит и через точку B.
–Б. Если окружность с центром O проходит через точку A, то она обязательно проходит и через точку C.
+В. Если точка O лежит на серединном перпендикуляре к отрезку AC, то она обязательно лежит и на серединном перпендикуляре к отрезку BC.
–В. Если точка O лежит на серединном перпендикуляре к отрезку AC, то точка O — обязательно центр окружности, вписанной в треугольник ABC.
+Г. Если точка O — центр окружности, описанной около треугольника ABC, то точка O обязательно лежит на серединном перпендикуляре к отрезку BC.
–Г. Если точка O — центр окружности, описанной около треугольника ABC, то точка O обязательно лежит на биссектрисе угла C.
3-й уровень
7. Даны две окружности с радиусами r1 и r2 (r1 > r2). Обозначим центры окружностей O1 и O2 соответственно. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Если окружности имеют только одну общую касательную, то O1O2 = r1 – r2.
–А. Если окружности имеют только одну общую касательную, то O1O2 = r1 + r2.
+Б. Если окружности имеют ровно две общие касательные
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.