Равенство: Вариативные тестовые вопросы по геометрии (Варианты 1-4 по 12 вопросов)

Вариант 1

Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите . Если хотя бы одна буква из 4х будет не отмечена, задание считается невыполненным.

1. Отрезки AB и CD пересекаются в точке O (см. рисунок). Известно, что AO = DO = 6 см, CO = OB = 5 см. Выберите правильное утверждение. А. ∆AOD = ∆COB. Б. ∆AOC = ∆DOB.

В. Отрезок CO — медиана треугольника  ABC.

Г. Треугольник COA равносторонний.

2. Отрезки AB и CD пересекаются в точке O, которая является серединой каждого из них (см. рисунок). Известно, что ÐAOC = 80°. Выберите правильное утверждение. А. ∆AOC = ∆ВОD. Б. Все углы треугольника СОВ острые.

В. Отрезок CO — высота треугольника  ABC.

Г. Отрезок AO — высота треугольника CAD.

3. Перпендикулярные отрезки MN и KP пересекаются в точке O, которая является серединой отрезка KP (см. рисунок). Известно, что MO = 10 см, ON = 9 см. Выберите правильное утверждение.

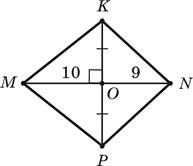
А. Медиана и высота треугольника MKN, проведенные из вершины K, совпадают.

Б. ∆MOK = ∆NOK.

В. ÐMOK> ÐKON.

Г. ∆MOK = ∆MOP.

4. Отрезок ACпересекает биссектрису угла ABC в точке P. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

А. Отрезки АВ и ВС обязательно равны.

Б. Угол ВРС может быть острым.

В. Если АB = BС, то прямые АC и РВ перпендикулярны.

Г. Если ÐBPA = 90°, то треугольник АВС равнобедренный.

5. Отрезки AB и CD пересекаются в точке O. Известно, что ∆AOC = ∆BOC (AO = BO,AC = BC). Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

А. Угол ВOD может быть тупой.

Б. Отрезки CO и OD обязательно равны.

В. Треугольники ACD и BCD обязательно равны.

Г. Отрезок CO обязательно является биссектрисой треугольника ACB.

6. Точка O — середина стороны ABтреугольника ABC (см. рисунок). Известно, что ÐCOB = 91°. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

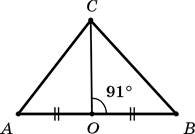
А. Отрезок CO — высота треугольника ACB.

Б. ÐА = ÐВ.

В. Треугольник ACB равносторонний.

Г. Отрезки АС и СВ равны.

7. Отрезки ABи CD пересекаются в точке O. Известно, что ÐAOC = ÐBOC. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

А. Треугольник ABD обязательно равнобедренный.

Б. Отрезок DO обязательно является высотой треугольника ADB.

В. Треугольники AOD и BOD обязательно равны.

Г. Отрезок ВО может быть биссектрисой треугольника DBC.

8. В треугольнике ABC известны две стороны: AB = 10 см, BC = 12 см. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

А. Угол A может равняться углу C.

Б. Если АС = 10 см, то ÐB = ÐС.

В. Если АС = 12 см, то ÐА = ÐВ.

Г. Если периметр треугольника АВС равняется 32 см, то ÐА = ÐВ.

9. На стороне AB треугольника ABC взята точка O (см. рисунок). Известно, что AO = 30 см, OB = 29 см, ÐAOC = 90°. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. АС = ВС. Б. Отрезок СО — биссектриса треугольника АВС.

В. Биссектриса угла ACB пересекает отрезок AO.

Г. Медиана и высота треугольника СОА, проведенные из вершины С, совпадают.

10. Отрезки AB и CD лежат на прямой m (см. рисунок). Точка N не лежит на прямой m. Известно, что  AB = NC = 16 см, BN = CD = 15 см. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

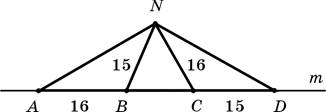
А. Высоты треугольников BNC и AND, проведенные из вершины N, обязательно совпадают.

Б. Медианы треугольников BNC и AND, проведенные из вершины N, обязательно совпадают.

В. Отрезки AN и ND обязательно равны.

Г. Середина отрезка BC может лежать на биссектрисе угла BNC.

11. Точки R и S лежат в разных полуплоскостях, на которые прямая PQ разбивает плоскость. Известно, что PR = SQ, RQ = PS. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.

А. Углы RPQ и PQS обязательно равны.

Б. Луч PQ обязательно является биссектрисой угла SPR.

В. Медиана треугольника PRQ, проведенная из вершины R, может лежать на биссектрисе угла PSQ.

Г. Середина отрезка PQ обязательно лежит на прямой RS.

12. Отрезки KL и MN пересекаются в точке Q. Известно, что KQ = NQ, ÐMKL = ÐMNL.

А. Отрезок QM может быть длиннее отрезка QL.

Б. Углы QML и QLM обязательно равны.

В. Медианы треугольников KQN и MQL, проведенные из вершины Q, обязательно лежат на одной прямой.

Г. Точка Q обязательно лежит на отрезке, соединяющем середины отрезков ML и KN.

Вариант 2

Записывая ответы на задания теста, обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными. Например, если вы считаете правильными утверждения А и В, а неправильными — утверждения Б и Г, запишите . Если хотя бы одна буква из 4х будет не отмечена, задание считается невыполненным.

1. На стороне AB треугольника  ABC взята точка O (см. рисунок). Известно, что AO = OB = 6 см,AC = 10 см, CB = 11 см. Выберите правильное утверждение. А. Треугольник АВС равнобедренный.

Б. Отрезок СО — медиана треугольника АВС.

В. ∆AOC = ∆ВОС.

Г. Периметры треугольников AOC и ВОС равны.

2. Отрезки KM и NL пересекаются в точке O, которая является серединой каждого из них. Известно, что KL = 15 см, KN = 14 см. Выберите правильное утверждение. А. ∆KOL = ∆MON. Б. ML >14 см. В. NM < 15 см. Г. ML = 15 см.

3. Отрезки PQ и RS пересекаются в точке O (см. рисунок), причем PO = OQ. Известно, что ÐROQ = 90°, RQ = 10 см, SQ = 11 см. Выберите правильное утверждение.

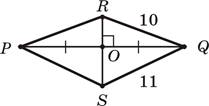
А. PR = 11 см.

Б. PS = 10 см.

В. Отрезок OQ — биссектриса треугольника RQS.

Г.  Медиана и высота треугольника PQR, проведенные из вершины R, совпадают