Геометрия 11 класс. Тема: Комбинации геометрических тел
Цель данного теста — проверить, умеет ли учащийся:
¾ распознавать простейшие комбинации многогранников и тел вращения;
¾ применять основные свойства многогранников, вписанных в шар и описанных около шара при решении задач;
¾ применять основные свойства призм, вписанных в цилиндр и описанных вокруг цилиндра для решения задач;
¾ применять основные свойства пирамид, вписанных в конус и описанных вокруг конуса для решения задач;
¾ решать задачи на комбинацию пространственных фигур.
Вариант 1
Записывая ответы на задания теста,
обведите буквы, отвечающие утверждениям, которые вы считаете правильными, и
зачеркните буквы, отвечающие утверждениям, которые вы считаете неправильными.
Например, если вы считаете правильными утверждения А и В, а
неправильными — утверждения Б и Г, запишите ![]()
![]()
![]()
![]() .
Если хотя бы одна буква из 4-х будет не
отмечена, задание считается невыполненным.
.
Если хотя бы одна буква из 4-х будет не
отмечена, задание считается невыполненным.
1-й уровень
1. Сфера с центром O описана около призмы ABCA1 B1 C1, причем O1 и O2 — центры окружностей, описанных около оснований. Выберите правильное утверждение.
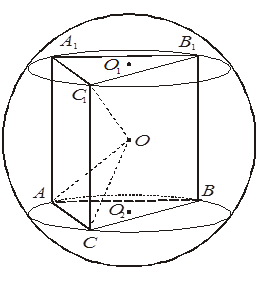
+А. Все вершины призмы лежат на данной сфере.
–Б. OA < OC.
–В. OO1 > OO2.
–Г. OC > OC1.
2. Цилиндр вписан в правильную четырехугольную призму ABCDA1B1C1D1, со стороной основания a. Выберите правильное утверждение.
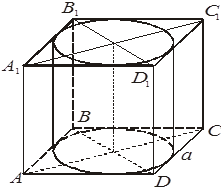
–А. Высота цилиндра меньше высоты призмы.
+Б. Основанием комбинации тел является круг, вписанный в квадрат.
–В. Диаметр основания цилиндра меньше стороны квадрата ABCD.
–Г. Радиус основания цилиндра меньше ![]() .
.
3. Шестиугольная пирамида SABCDEF вписана в конус, причемO — центр окружности, описанной около основания пирамиды. Выберите правильное утверждение.
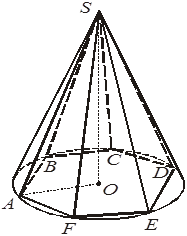
–А. Высота конуса больше SO.
–Б. Боковое ребро SA пирамиды больше образующей конуса SB.
+В. Основанием пирамиды является шестиугольник, около которого можно описать окружность.
–Г. AC — радиус окружности, описанной около основания призмы.
2-й уровень
4. Шар с центром O1 вписан в правильную треугольную пирамиду SABC с двугранным углом a при основании и его линейным углом SMO. Точка O — точка касания шара и грани ABC. Отметьте, какие из приведенных четырех утверждений правильные, а какие — неправильные.
+А. Точка O – центр окружности, вписанной в основание пирамиды.
–А. Точка O не совпадает с центром окружности, вписанной в основание пирамиды.
+Б. Центр шара O1 лежит на высоте SO пирамиды.
–Б. Центр шара O1 не лежит на высоте SO пирамиды.
+В. MO1 является биссектрисой угла SMO.
–В. MO1 не совпадает с биссектрисой угла SMO.
+Г. Радиус шара OO1 равен ![]() .
.
–Г. Радиус шара OO1 равен ![]() .
.
5. Цилиндр описан около треугольной призмы высотой H, основанием которой является прямоугольный треугольник с гипотенузой c. Отметьте, какие из приведенных четырех утверждений правильные, а какие — неправильные.
+А. В основании комбинации тел лежит прямоугольный треугольник, вписанный в круг.
–А. В основании комбинации тел лежит прямоугольный треугольник, описанный около круга.
+Б. Центр основания цилиндра принадлежит наибольшей боковой грани призмы.
–Б. Центр основания цилиндра принадлежит наименьшей боковой грани призмы.
+В. Радиус цилиндра равен ![]() .
.
–В. Радиус цилиндра больше ![]() .
.
+Г. Боковая поверхность цилиндра равна pcH.
–Г. Боковая поверхность цилиндра равна 2pcH .
6. Конус вписан в правильную четырехугольную пирамиду со стороной основания a и апофемой h. Отметьте, какие из приведенных четырех утверждений правильные, а какие — неправильные.
+А. В основании комбинации тел лежит окружность, вписанная в квадрат.
–А. Основанием комбинации тел является окружность, описанная около квадрата.
+Б. Радиус основания конуса равен ![]() .
.
–Б. Радиус основания конуса больше ![]() .
.
+В. Образующая конуса равна апофеме пирамиды.
–В. Образующая конуса равна боковому ребру пирамиды.
+Г. Площадь боковой поверхности конуса равна ![]() .
.
–Г. Площадь боковой поверхности конуса больше ![]() .
.
3-й уровень
7. Шар описан около правильной четырехугольной пирамиды, сторона основания которой и высота равняются a. Отметьте, какие из приведенных четырех утверждений правильные, а какие — неправильные.
+А. Сечением комбинации тел плоскостью, проходящей через высоту пирамиды и диагональ основания пирамиды, является диагональное сечение пирамиды, вписанное в большой круг шара.
–А. Сечением комбинации тел плоскостью, проходящей через высоту пирамиды
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.