–Б. После подстановки y через x во второе уравнение системы можно получить уравнение 3x2 – x(2 – 3x) = –2.
+В. Уравнение, полученное после подстановки y через x во второе уравнение, имеет единственый корень x = 1.
+Г. Заданная система имеет
единственное решение 
7. Задана система 
Отметьте, какие из следующих
четырех утверждений правильные, а какие — неправильные.
+А. Для
построения графиков уравнений системы ее можно представить так: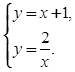 
+Б. Графики уравнений заданной
системы изображаются так:
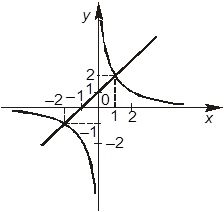
–В. Графики уравнений заданной
системы изображаются так:
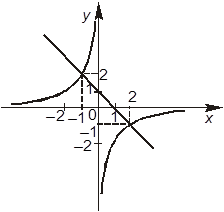
+Г. Система имеет решения: 
8. Задана система 
Отметьте,
какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. После умножения второго уравнения системы на 2 и почленного сложения с первым уравнением можно получить уравнение 2x2 + 5x – 7 = 0.
–Б. Уравнение,
полученное после умножения второго уравнения системы на 2 и почленного
сложения с первым уравнением, имеет корни x = –1 и x = 
.
+В. Заданная система уравнений
равносильна совокупности систем:
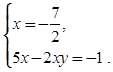
–Г. Заданная система имеет только такие решения: 
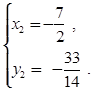
9. У двузначного числа цифра десятков на 1 больше цифры единиц, а произведение его цифр на 45 больше утроенного числа его десятков. Цифру десятков заданного числа обозначили через x, а цифру единиц — через y. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
–А. По условию можно составить
такую систему 
+Б. Система, составленная по условию, имеет два разнличных решения.
+В. Условию удовлетворяет только одно двузначное число.
–Г. Заданное двузначное число меньшее 90.
10. Задано уравнение 3x + x3 = 14. Его левую часть обозначили через f (x): f (x) = 3x + x3. Пользуясь свойством возрастающей функции*, отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Заданное уравнение может иметь только один корень.
–Б. Функция f (x) может равняться 14 при двух значениях аргумента x.
+В. f (2) = 14.
+Г. Единственным корнем заданного уравнения является x = 2.
11. Чтобы найти количество решений
системы 
где a — некоторое число, построили график
каждого из уравнений системы. Отметьте, какие из следующих четырех утверждений
правильные, а какие — неправильные.
+А. При различных значениях a (a ¹ 0) графики уравнения y = x + a — это прямые, параллельные графику функции y = x.
–Б. График первого уравнения — окружность радиуса 4 с центром в начале координат.
+В. Прямая y = x + a касается окружности x2 + y2 = 4 при a = 2
и при a = –2.
+Г. Система имеет единственное решение при a = 2 и при a = –2.
12. Задана система 
Отметьте, какие из следующих
четырех утверждений правильные, а какие — неправильные.
+А. Чтобы получить уравнение, которое можно рассматривать как квадратное относительно x или y, можно второе уравнение умножить на 4 и почленно вычесть результат из первого уравнения системы.
–Б. Если уравнение x2 – 4xy + 3y2 = 0 (полученное в результате умножения второго уравнения системы на 4 и почленного вычитания) решить относительно x, то по формуле корней квадратного уравнения можно получить x = –2y ± y.
+В. Заданная система
равносильна совокупности двух систем:
+Г. Заданная система имеет
только такие решения: 
Ответы к тестам
* Возрастающая функция может принимать каждое свое значение только при одном значении аргумента.
* Возрастающая функция может принимать каждое свое значение только при одном значении аргумента.
* Возрастающая функция может принимать каждое свое значение только при одном значении аргумента.
*Возрастающая функция может принимать каждое свое значение только при одном значении аргумента.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.