|
2. Чтобы определить количество решений системы –А. Система не имеет решений. –Б. Система имеет одно решение. +В. Система имеет два решения. –Г. Система имеет четыре решения. |
|
3. Чтобы решить систему ![]() во второе
уравнение подставили y = x + 3. Выберите, какой вид будет иметь второе уравнение после
этой подстановки.
во второе
уравнение подставили y = x + 3. Выберите, какой вид будет иметь второе уравнение после
этой подстановки.
+А. 2x2 + 7x – 4 = 0.
–Б. x2 + 7x – 4 = 0.
–В. 2x2 + 7x + 4 = 0.
–Г. 2x2 – 7x + 4 = 0.
4. Даны изображения графиков функций: y = x2 + 1, y = 2 – x, y = x + 2.
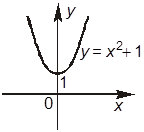
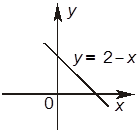
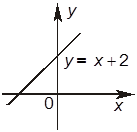
Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Функция y = x + 2 возрастает при всех значениях x.
–Б. Функция y = 2 – x возрастает при всех значениях x.
–В. Функция y = x2 + 1 возрастает при всех значениях x.
+Г. Функция y = x2 + 1 возрастает только при x ³ 0.
|
5. Чтобы графически решить систему +А. Одним из решений заданной системы являются координаты точки A. +Б. Одним из решений заданной системы являются координаты точки В. –В. Одним из решений заданной системы являются координаты точки С. |
|
+Г. Решениями системы являются
![]()
![]()
6. Задана система ![]() Отметьте,
какие из следующих четырех утверждений правильные, а какие — неправильные.
Отметьте,
какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Из первого уравнения y через x выражается так: y = 5 – x.
–Б. После подстановки y через x во второе уравнение системы можно получить уравнение x2 + x(5 + x) = 10.
–В. Уравнение, полученное после подстановки y через x во второе уравнение, имеет два корня.
+Г. Заданная система имеет
единственное решение ![]()
7. Задана
система ![]() Отметьте, какие из следующих
четырех утверждений правильные, а какие — неправильные.
Отметьте, какие из следующих
четырех утверждений правильные, а какие — неправильные.
–А. Для построения графиков
уравнений системы ее можно представить так: 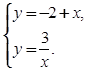
–Б. Графики уравнений заданной
системы изображаются так:
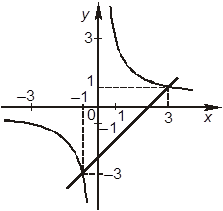
+В. Графики уравнений заданной
системы изображаются так:
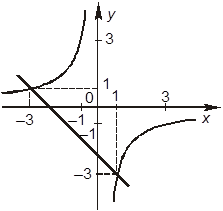
+Г. Система имеет решения: ![]()
![]()
8. Задана система ![]() Отметьте,
какие из следующих четырех утверждений правильные, а какие — неправильные.
Отметьте,
какие из следующих четырех утверждений правильные, а какие — неправильные.
–А. После умножения второго уравнения системы на 3 и почленного сложения с первым уравнением можно получить уравнение 3x2 + 4x – 1 = 0.
–Б. Уравнение,
полученное после умножения второго уравнения системы на 3 и почленного сложения с первым
уравнением, имеет корни x = 1 и x = ![]() .
.
+В. Заданная система уравнений
равносильна совокупности систем: ![]()
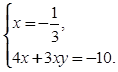
+Г. Заданная система имеет только такие решения: ![]()

9. С двух пунктов, расстояние между которыми равняется 24 км, вышли одновременно навстречу друг другу два туриста и встретились через 2,4 часа. Известно, что первый турист проходит весь путь 24 км на 2 часа быстрее, чем второй. Скорость первого туриста обозначили через x км/ч, а второго — через y км/ч. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные.
+А. Если туристы двигаются навстречу друг другу, то они сближаются со скоростью (x + y) км/ч.
–Б. По условию можно составить такую систему 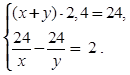
+В. Система,
составленная по условию, равносильна системе ![]()
–Г. Второй турист пройдет весь путь 24 км за 4 часа.
10. Задано уравнение 2x + ![]() = 21. Его левую часть обозначили
через f (x): f (x) = 2x +
= 21. Его левую часть обозначили
через f (x): f (x) = 2x + ![]() . Пользуясь свойством возрастающей функции*, отметьте, какие из следующих четырех утверждений правильные,
а какие — неправильные.
. Пользуясь свойством возрастающей функции*, отметьте, какие из следующих четырех утверждений правильные,
а какие — неправильные.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.