Алгебро-логические свойства R-функций. Дифференциальные свойства R-функций. Алгоритмически полные системы R-функций

4. Алгебро-логические свойства R-функций

Поскольку одна и та же сопровождающая функция является сопровождающей для различных R-функций одной и той же ветви, то, вообще говоря, на R-функции не переносятся автоматически тождества, известные из булевой алгебры. Например, как было уже выяснено, R-функция  положительна, когда знаки аргументов совпадают, и сопровождающей для неё будет булева функция равнозначности . Но эта функция связана с дизъюнкцией и конъюнкцией тождеством: . Заменив в этом равенстве булевы операции соответствующими R-функциями, найдём для системы R_a:

.

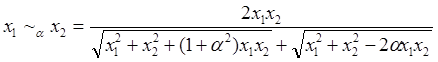Таким образом, хотя знаки и соответствуют значениям сопровождающей функции, сами числовые значения R-функций могут не удовлетворять тождествам, известным из булевой алгебры.

Тем не менее, R-функции обладают рядом свойств, сходных со свойствами сопровождающих их функций алгебры логики. Ниже приводятся те тождества, которые справедливы для основных систем. Их доказательство предоставляется выполнить самостоятельно.

1. Закон двойного отрицания:.
2.  - коммутативность R-конъюнкции.
3.  - коммутативность R-дизъюнкции.
4.  

.

5. .
6. 
7. 
8.  или .
9.  или .

Два последних свойства показывают, в каких случаях обращаются в нуль R-конъюнкция и R-дизъюнкция двух переменных. В дальнейшем на основе этого свойства мы покажем, что суперпозиция нескольких R-конъюнкций всегда является предикатом выпуклой области.

Следующие свойства выполняются только при a=1:

Заметим, что свойства ассоциативности и дистрибутивности R-функций (14-17) выполняются только в системе R₁ и не выполняются в других системах.

Приведенные системы являются достаточно полными, т.е. их суперпозицией можно образовать R-функцию для любой сопровождающей булевой функции.

5. Дифференциальные свойства R-функций

Функции, получающиеся в результате суперпозиции приведенных основных систем, обладают рядом важных дифференциальных свойств, которые в дальнейшем будут использоваться при построении уравнений сложных геометрических объектов и структур решений краевых задач.

Рассмотрим произвольное достаточное число раз дифференцируемое отображение  и R-функцию . Их композиция , вообще говоря, не является R-функцией. Однако она обладает некоторыми дифференциальными свойствами отображения .

Теорема о производной R-конъюнкции.Если , причём в некоторой точке x₀ , а , то при произвольном дифференцируемом  производная по любому направлению от R_a-конъюнкции  в точке x₀ равна производной от .

Доказательство проведём путём непосредственного дифференцирования формулы, определяющей R_a-конъюнкцию:

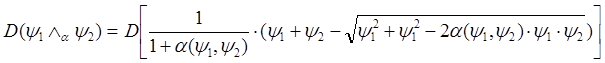, где D – оператор дифференцирования  по направлению. Вычислим производную:

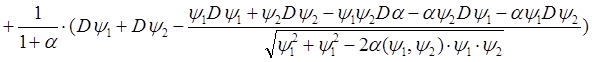, откуда в силу условия x₀  при x=x₀ получаем:

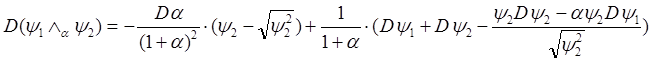, но поскольку в этой точке , то ; после упрощений имеем:

.

Теперь рассмотрим аналогичное дифференциальное свойство R-дизъюнкции.

Теорема о производной R-дизъюнкции.Если , причём в некоторой точке x₀ , а , то при произвольном дифференцируемом  производная по любому направлению от R_a-дизъюнкции  в точке x₀ равна производной от .

Доказательство проведём аналогично доказательству предыдущей теоремы:

.

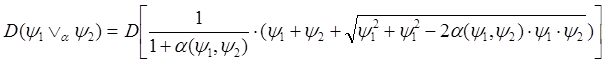Вычислим производную:

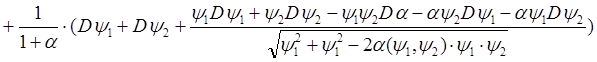, откуда в силу условия x₀  при x=x₀ получаем:

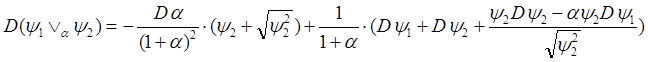, но поскольку в этой точке , то ; после упрощений имеем:

.

Приведем также (без доказательства) сходную теорему об R - эквивалентности.

Теорема о производной R-эквивалентности.Если в условиях предыдущих теорем в точке x₀ , а , то производная  в точке x₀ равна производной от , умноженной на sign .

Очевидно также, что производная R-отрицания равна R-отрицанию производной (т.е. производной, взятой с противоположным знаком).

Все эти результаты можно обобщить в виде следующей теоремы, сформулированной и доказанной В.Л. Рвачёвым:

Теорема о производной R-функции с единственным вхождением аргумента. Пусть  есть суперпозиция функций (-1), х, , , имеющая единственное вхождение аргумента  с инверсной степенью (числом операций отрицания над  и содержащими  частями) s, а функция  - произвольная дифференцируемая функция, причём в некоторой точке  , а , i=2,…,m. Тогда если , то справедливо равенство:

.

Доказательство.