Обозначим ![]() (результат k-кратного применения операции R-отрицания
к переменной f). Воспользуемся формулой
(результат k-кратного применения операции R-отрицания
к переменной f). Воспользуемся формулой ![]() для исключения из формулы
для исключения из формулы ![]() операции R-дизъюнкции.
Ввиду того, что
операции R-дизъюнкции.
Ввиду того, что ![]() имеет единственное
вхождение в формулу
имеет единственное
вхождение в формулу ![]() , её можно представить
в виде:
, её можно представить
в виде: ![]() , где p, q – некоторые выражения, не содержащие
, где p, q – некоторые выражения, не содержащие ![]() . Сумма
. Сумма ![]() . Согласно условию теоремы
. Согласно условию теоремы ![]() , откуда
, откуда ![]() . Поскольку p и q получены с помощью операций R-конъюнкции,
R-дизъюнкции и R-отрицания
только из ненулевых аргументов
. Поскольку p и q получены с помощью операций R-конъюнкции,
R-дизъюнкции и R-отрицания
только из ненулевых аргументов ![]() , то они не
равны нулю в точке x0.
Исходя из алгебро-логических свойств R-конъюнкции, в
этой точке
, то они не
равны нулю в точке x0.
Исходя из алгебро-логических свойств R-конъюнкции, в
этой точке ![]() ,
, ![]() ;
точно так же
;
точно так же ![]() ,
, ![]() . Но в силу теоремы о производной
R-конъюнкции получаем:
. Но в силу теоремы о производной
R-конъюнкции получаем:
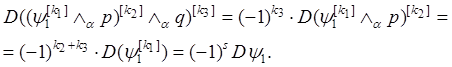
Для некоторых систем R-функций справедливы и более сильные теоремы.
Рассмотрим, далее, некоторые свойства, касающиеся вторых производных от R-конъюнкций и R-дизъюнкций, которые понадобятся для выяснения выпуклости и вогнутости графиков R-функций.
Лемма. Если ![]() -
однородная функция измерения 1 (т.е.
-
однородная функция измерения 1 (т.е. ![]() ), причём
), причём 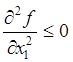
![]() ,
и
,
и ![]() , где
, где ![]() -
биекция числовой оси на положительную и отрицательную полуоси, то функция f не убывает по каждому из аргументов.
-
биекция числовой оси на положительную и отрицательную полуоси, то функция f не убывает по каждому из аргументов.
Доказательство. Используем формулу Эйлера для однородных функций:
![]() .
.
Продифференцируем это равенство по ![]() и
и ![]() :
:
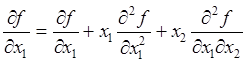 , откуда
, откуда 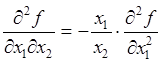 ;
;
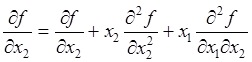 , откуда
, откуда 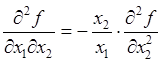 ;
;
следовательно, 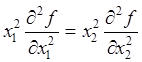 . Тогда из неравенства
. Тогда из неравенства 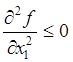 следует
следует 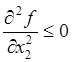 .
.
Из тождества ![]() , пользуясь
свойствами R-конъюнкции, имеем:
, пользуясь
свойствами R-конъюнкции, имеем: ![]() при
при ![]() ,
,
![]() или при
или при ![]() ,
, ![]() ;
;
![]() при
при ![]() и
и
![]() ; в остальных случаях
; в остальных случаях ![]() . Тогда
. Тогда 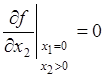 . Но в первом квадранте
. Но в первом квадранте ![]() - возрастающая функция
- возрастающая функция ![]() при фиксированном
при фиксированном ![]() , поскольку
, поскольку 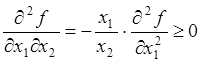 ; следовательно,
; следовательно, ![]() в первом квадранте. Аналогично
легко показать справедливость этого неравенства и во втором квадранте (рисунок
4).
в первом квадранте. Аналогично
легко показать справедливость этого неравенства и во втором квадранте (рисунок
4).
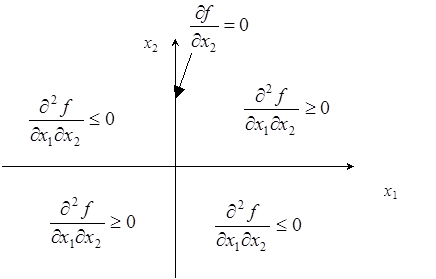
Рисунок 4. К доказательству леммы о второй производной.
Далее, поскольку при![]() ,
,
![]() f=0, производная
f=0, производная 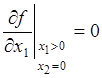 . Но
. Но ![]() - убывающая функция
- убывающая функция ![]() при фиксированном
при фиксированном ![]() в 4-м квадранте и возрастающая –
в первом. Следовательно, в первом и четвертом квадранте справедливо
неравенство:
в 4-м квадранте и возрастающая –
в первом. Следовательно, в первом и четвертом квадранте справедливо
неравенство: ![]() .
.
Точно так же, используя условия: 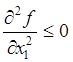 и
и
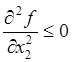 , получаем, что
, получаем, что ![]() и
и ![]() в
остальных квадрантах.
в
остальных квадрантах.
Доказанная лемма служит основой для двух важных теорем.
Теорема о второй производной R-конъюнкции. Если ![]() удовлетворяет
условиям леммы, а функция
удовлетворяет
условиям леммы, а функция ![]() , причём
вторая производная
, причём
вторая производная ![]() по произвольному
направлению l, то
по произвольному
направлению l, то ![]() .
.
Доказательство в предположении о выпуклости функции f можно получить, непосредственно дифференцируя ![]() дважды по l:
дважды по l:
![]() ;
;
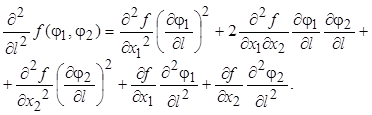
Поскольку ![]() ,
, ![]() , квадратичная форма со вторыми
производными неположительна, из последнего равенства получается
, квадратичная форма со вторыми
производными неположительна, из последнего равенства получается ![]() .
.
Условиям теоремы о второй производной удовлетворяет, в
частности, ![]() -конъюнкция.
-конъюнкция.
Выше было на интуитивном уровне введено понятие чертежа – точечного множества, обобщающего такие понятия, как «линия», «поверхность», «тело», «гиперповерхность» и т.п. Простейшим чертежом является точка, и поэтому чертежи можно было бы рассматривать как совокупности точек, т.е. элементы множества всех подмножеств R n. Однако тогда пришлось бы считать чертежами и такие геометрические объекты, о форме которых можно говорить только весьма условно.
Будем называть чертежом множество точек в R n, координаты которых удовлетворяют уравнениям вида f(x)=0, где f –функция из достаточно общего множества. В аналитической геометрии часто рассматривают алгебраические (целые рациональные) функции; это приводит к алгебраическим чертежам. К их числу относятся алгебраические кривые и поверхности второго порядка. Для простоты будем называть уравнение чертежа непрерывным, дифференцируемым, аналитическим и т.д., если функция f является соответственно непрерывной, дифференцируемой, аналитической и т.д.
Множество алгебраических чертежей не содержит таких часто
встречающихся линий и поверхностей, как квадрат, ломаная линия, усеченный конус
и других объектов более сложной формы (например, материнская плата компьютера).
Напротив, если потребовать только непрерывности уравнения, то класс чертежей
получается излишне широким. В этом случае уравнению f(x)=0 соответствует замкнутое множество точек в Rn, и обратно: всякому замкнутому точечному
множеству L соответствует (не единственное)
непрерывное уравнение, одно из которых – уравнение ![]() .
Это уравнение называется нормальным уравнением чертежа L.
.
Это уравнение называется нормальным уравнением чертежа L.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.