ПРИЛОЖЕНИЕ 1
Если перед нами выборка случайной величины, то протокол наблюдений должен быть «однородным». Иногда это видно «на глаз». Но в сомнительных случаях дело проясняет «сглаживание». Простейшее сглаживание – это сглаживание «скользящими средними» по трем, пяти и более точкам. Соответственно сглаженное значение в точке вычисляют как среднее из трех (пяти) значений:
![]() ;
; ![]() .
.
Если xi независимы
и представляют одну и ту же случайную величину, и имеют одну и ту же дисперсию![]() , то по теореме сложения
дисперсий стандартное отклонение (а, значит, и размах)
, то по теореме сложения
дисперсий стандартное отклонение (а, значит, и размах) ![]() , сглаженного по трем (пяти)
точкам будет соответственно:
, сглаженного по трем (пяти)
точкам будет соответственно:
![]() ;
; ![]() ;
;
то есть в 2 – 2,5 раза меньше, и «среднее» поведение xi будет «виднее».
Для сглаживания протокола из 100 точек xiпридется вычислить ![]() в точках i =
2, 3, …, 99. Но этих вычислений можно
избежать: трёхточечное скользящее среднее легко найти графически.
в точках i =
2, 3, …, 99. Но этих вычислений можно
избежать: трёхточечное скользящее среднее легко найти графически.
Рассмотрим фрагмент протокола (рис.1). Известно, что в треугольнике точка пересечения медиан делит их в отношении ( 1/3 ) : ( 2/3 ). Длина вертикальной медианы в треугольнике ( xi-1 , xi , xi+1 ) равна xi – (xi-1 + xi+1) / 2, отсюда ордината точки пересечения медиан равна среднему из трех точек:
![]()
![]() =
=![]() .
.
Точно так же находим пересечение медиан в следующих треугольниках
( xi , xi+1 , xi+2) и т.д. Треугольник ( xi+1 , xi+2 , x i+3 ) выродился в прямую,
поэтому точка ![]() совпадает с xi+2. Соединив
найденные точки, получим линию трехточечного скользящего среднего.
совпадает с xi+2. Соединив
найденные точки, получим линию трехточечного скользящего среднего.
Может случиться, линия ![]() недостаточно
гладкая – тогда ее сглаживают повторно тем же способом. Математически повторно
сглаженное значение
недостаточно
гладкая – тогда ее сглаживают повторно тем же способом. Математически повторно
сглаженное значение ![]() выражается формулой:
выражается формулой:
![]()
![]() =
=
=![]() , то
есть это средневзвешенное значение по 5 точкам. Если дисперсии всех xi одинаковы и равныs2, то
по теореме сложения дисперсий:
, то
есть это средневзвешенное значение по 5 точкам. Если дисперсии всех xi одинаковы и равныs2, то
по теореме сложения дисперсий:
![]() =
=![]() , или чуть хуже, чем расчетное
сглаживание по 5 точкам (см. выше).
, или чуть хуже, чем расчетное
сглаживание по 5 точкам (см. выше).
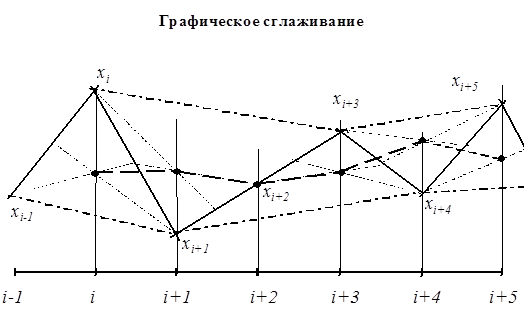 Рис. 1
Рис. 1
Проявление полос размаха
Иногда приходится «проявлять» и полосу размаха. Для этого на протоколе прочерчивают две ломаные линии: одну – по верхним точкам возврата, другую – по нижним. Верхняя точка возврата – точка, которая выше обеих соседних, нижняя точка возврата – точка, которая ниже обеих соседних.
В случае, если эти ломаные имеют большой размах, то их тоже приходится сглаживать аналогичным способом.
После небольшой тренировки графическое сглаживание по трем точкам не составляет особого труда ( 10 – 20 минут на 100 точек ). Точку пересечения медиан в простых треугольниках легко научиться с неплохой точностью ставить «на глаз», прибегая к графическим построениям только в «тяжелых» случаях (очень растянутый тупоугольный треугольник и т.п.).
Этот приём, многократно облегчает дальнейшие вычисления числовых характеристик. Суть его в том, что вводятся «условные» переменные (u,v), связанные с исходными переменными (x,y):
x=Cx+hxu; y=Cy+hyv,
где hx и hy – длины интервалов группировки;
Cy – «ложные нули».
Cx – одна из вариант ![]() (точки
середины интервалов разбивки по х), взятая обычно в «самой гуще».
Аналогично выбирается Cy.
(точки
середины интервалов разбивки по х), взятая обычно в «самой гуще».
Аналогично выбирается Cy.
Например, для «фонового массива» (см. табл. II.1):
выбор Cx=16.0 конкретизирует переход х®u при hx= 4.0
x=16.0+4.0u.
Теперь видно:
при u=0 получим середину четвёртого интервала варианту ![]() =16.0, при u=-1 получим середину третьего интервала варианту
=16.0, при u=-1 получим середину третьего интервала варианту ![]() =12.0, при u=1 получим середину пятого интервала варианту
=12.0, при u=1 получим середину пятого интервала варианту ![]() =20.0, и вообще изменение u на
+1(-1) отвечает переходу к следующей (предыдущей) варианте
=20.0, и вообще изменение u на
+1(-1) отвечает переходу к следующей (предыдущей) варианте ![]() .
.
Далее при расчёте числовых характеристик придётся вычислять
среднее значение ![]() степеней х
(k=1,2,3,4).
Операция «осреднения» линейна, поэтому имеет место соотношение
степеней х
(k=1,2,3,4).
Операция «осреднения» линейна, поэтому имеет место соотношение
![]() =
=![]() , а
вычислить
, а
вычислить ![]() значительно легче, поскольку u принимают «хорошие» значения 0;
значительно легче, поскольку u принимают «хорошие» значения 0; ![]() 1;
1;
![]() 2; и т.д. Впрочем, можно
проводить расчёты и в исходных данных.
2; и т.д. Впрочем, можно
проводить расчёты и в исходных данных.
Х=Ģ(m;s) - зависит от двух параметров m и s, где m – математическое
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.