









3. Расчёткотлацистерны.
Выбор расчётных схем для котлов цистерн, имеющих раму и безрамных конструкций должен учитывать особенности их работы. В частности, котлы безрамных цистерн воспринимают все виды расчётных нагрузок, предусмотренных «Нормами».
Котлы цистерны, установленные на рамах, практически не испытывают воздействие продольных нагрузок, передающихся через ударно-тяговые приборы. Эти нагрузки оказывают некоторое влияние лишь на зоны лап крепления котла к раме.
В тоже время, силы инерции в режиме «удар-рывок» могут вызвать заметное влияние на котлы, установленные на рамах, как через лапы, так и при догрузке вертикальной нагрузкой опорных устройств.
Во всех случаях нагружения для предварительных оценок приемлема балочная схема с последующим уточнением характеристик напряженного-деформированного состояния на основе интегрирования уравнений теории тонкостенных цилиндрических круговых оболочек.
Уточнения осуществляется за счёт учёта самоуравновешенных внутренних усилий, которые возникают из-за деформаций контура поперечных сечений.
Сечения по образующей называют продольными площадками, а по окружности-поперечными. Изгибающий момент в кольцевом направлении на продольных площадках обозначают как М2, а нормальную силу на поперечных площадках как N1. Они зависят от двух координат (обычно цилиндрических).
В расчётах по балочным схемам находят напряжения на поперечных площадках цилиндрической части котла, и они распределяются по высоте сечения по линейному закону. Эти напряжения соответствуют внутренним усилиям (изгибающему моменту и продольной силе), которые находят из условий равновесия расчётной схемы при абсолютно жестком контуре поперечного сечения котла-балки. Как уже отмечалось, дополнительные распределенные усилия N1 и M2 обусловлены деформациями контура поперечных сечений и относятся к числу самоуравновешенных, т.е. интеграл от которых по контуру сечения равен нулю.
Тогда суммарные напряжения на поперечных площадках будут определяться как
σ1=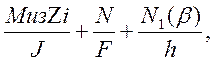 (3.1)
(3.1)
напряжения на продольных площадках
σ2=±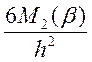 , (3.2)
, (3.2)
В этих формулах:
J-момент инерции кольцевого сечения: при осреднённой постоянной толщине оболочки h –
J=![]() ;
;
R-радиус срединной поверхности оболочки (поверхности, делящей толщину оболочки пополам);
Миз - изгибающий момент, в балке с жёстким контуром;
N -продольная сила в балке с жестким контуром;
F=2![]() -площадь сечения балки с кольцевым
сечением;
-площадь сечения балки с кольцевым
сечением;
М2(β) и N1(β)- самоуравновешенные дополнительные усилия;
Zi- расстояние от горизонтальной оси симметрии до точки на срединной поверхности кольцевого сечения zi=Rcosβi .
Выпишем уравнения
полубезмоментной теории, представленные в цилиндрической системе координат. При
этом в направлении x по образующей будем
пользоваться относительной координатой 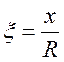 ,
а по окружности – угловой координатой β.
,
а по окружности – угловой координатой β.
Тогда
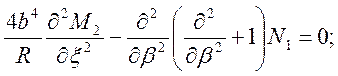 (3.3)
(3.3)
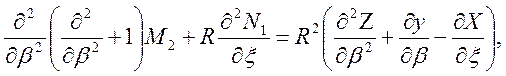
где
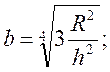 (3.4)
(3.4)
Z, Y и X – распределённые по поверхности нагрузки на оболочку котла, направленные Z-по радиусу (нормальные к поверхности), Y-по касательной к окружности и X-вдоль образующей.
Уравнения в частных производных (3.3) можно решить, используя метод Бубнова-Гарелкина.
Предварительно, зная схемы нагружения, т.е. определив, где и как распределены компоненты нагрузок, разложим их в двойные тригонометрические ряды
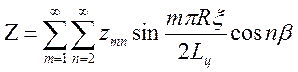 ;
;
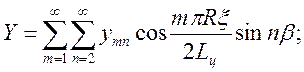 (3.5)
(3.5)
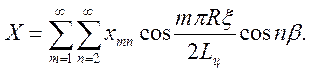
Здесь zmn, ymn, xmn-известные коэффициенты разложения в ряд Фурье заданных нагрузок; m и n-номера членов ряда;
m-принимаются нечётными в случае симметричного, относительно среднего сечения, m=1, 3, 5.
n-отсчитываются с 2 и далее, учитывая необходимость отыскания самоуравновешенных дополнительных усилий. Номер n=0 и n=1 соответствует балочному нагружению;
2Lц-длина цилиндрической части.
Коэффициенты zmn, ymn, xmn подсчитываются по формулам Фурье:
zmn=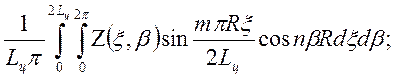
ymn=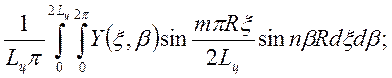 (3.6)
(3.6)
xmn=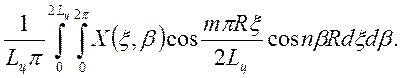
Представим неизвестные величины М2 и N1 рядами
M2=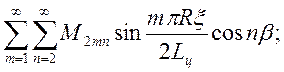
(3.7)
N1=![]()
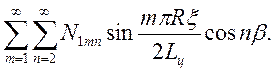
которые отвечают граничным условиям, т.е. при x=0 и x=2Lц,М2=0 и N1=0 и условиям периодичности по координате β.
Коэффициенты этих рядов М2mn и N1mn-неизвестны.
После подставки (3.5) с
учётом (3.6) и (3.7) в уравнения (3.3) и выполнения операций, предусмотренных
методом Бубнова-Гарелкина, получим алгебраические уравнения относительно
коэффициентов рядов M2mn и N1mn. При этом введём обозначения 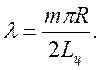
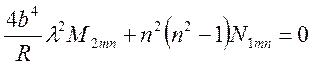 ;
;
(3.8)
![]()
Решив систему (3.8),найдём коэффициенты
![]()
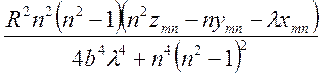 ;
;
(3.9)
![]()
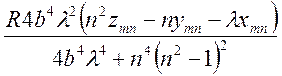 ;
;
Подставив (3.9) в формулу
(3.7) и выполнив суммирование рядов при фиксированных координатах ![]() и
и ![]() ,
определим значения дополнительных, связанных с изгибом контура поперечных
сечений, усилий в выбранных точках.
,
определим значения дополнительных, связанных с изгибом контура поперечных
сечений, усилий в выбранных точках.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.