Коржин С.Н. МИИТ
Меланин В.М.
Применение метода коечных элементов для анализа напряжений в клиновом гасителе колебаний
Для проведения анализа напряжений клинового гасителя колебаний использован метод конечных элементов (МКЭ).
МКЭ широко применяется во многих научных и инженерных приложениях. Основная идея МКЭ состоит в том, что рассматриваемая конструкция разделяется на ряд простейших по форме частей – элементов. Разбиение конструкции на конечные элементы является первой операцией метода конечных элементов. Несовершенное разбиение будет приводить к значительным погрешностям расчета, если даже все операции метода выполнены с достаточной точностью.
Для аппроксимации геометрии клина из библиотеки программы ANSYS был выбран объемный 10-ти узловой квадратичный конечный элемент в виде тетраэдра (рис 1).
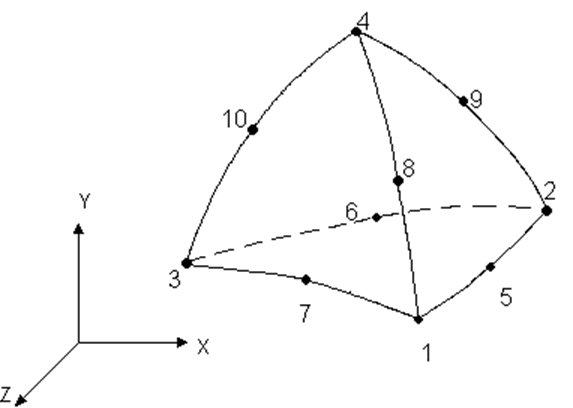 |
Рисунок 1.
Поле поступательных перемещений внутри конечного элемента описывается функцией формы в виде полного полинома второго ряда с десятью универсальными координатами, то есть всего 30-ть поступательных степеней свободы, по три в каждом узле . Связи между перемещениями в произвольной точке элемента и узлах заданы следующим способом :
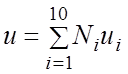
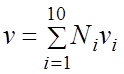
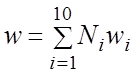
где Ni (i = 1, 2, … 10) - интерполяционные функции, которые в системе
естественных координат представлены следующими выражениями:
![]()
![]()
![]()
![]()
![]() ;
;
![]() ;
;![]() ;
;![]() ;
;![]()
![]()
где
ui , vi и wi – узловые поступательные перемещения (степени свободы) вдоль осей X, Y и Z соответственно;
![]() ,
, ![]() ,
, ![]() и
и ![]() - нормализованные координаты,
возрастающие от 0.0 в вершине к 1.0 на противоположной стороне или грани.
- нормализованные координаты,
возрастающие от 0.0 в вершине к 1.0 на противоположной стороне или грани.
|
Узел |
L1 |
L2 |
L3 |
L4 |
|
1 |
1 |
0 |
0 |
0 |
|
2 |
0 |
1 |
0 |
0 |
|
3 |
0 |
0 |
1 |
0 |
|
4 |
0 |
0 |
0 |
1 |
|
5 |
½ |
1/2 |
0 |
0 |
|
6 |
0 |
1/2 |
1/2 |
0 |
|
7 |
½ |
0 |
1/2 |
0 |
|
8 |
½ |
0 |
0 |
1/2 |
|
9 |
0 |
1/2 |
0 |
1/2 |
|
10 |
0 |
0 |
1/2 |
1/2 |
Далее используя формулы Коши , определяется вектор деформации следующим образом
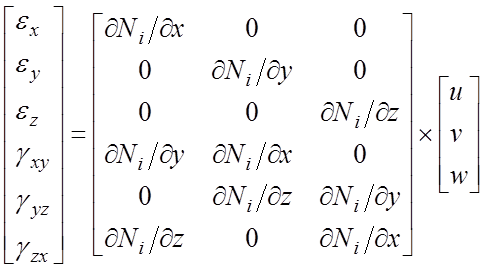 ,
,
где
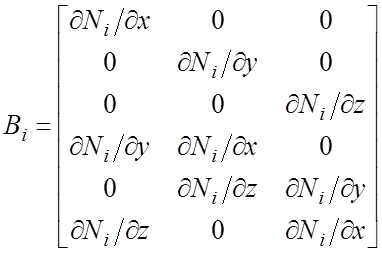 - матрица градиентов.
- матрица градиентов.
Для вычисления матрицы жесткости [Ke] используют, как правило, известную формулу:
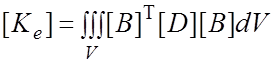
где [D] - матрица упругих характеристик материала
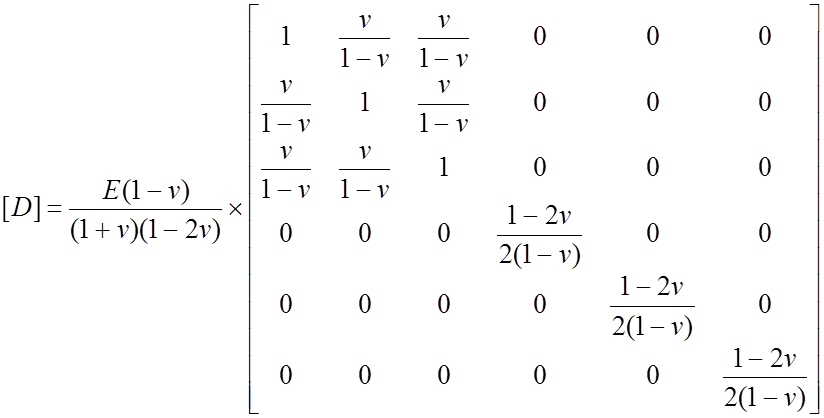
Так как вся конструкция состоит из совокупности элементов, то матрицы жесткости отдельных конечных элементов объединяются в суммарную матрицу, характеризующую всю систему.
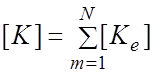
где N - число конечных элементов в системе.
Разрешающая система алгебраических уравнений метода конечных элементов в матричной записи принимает следующий вид:
![]()
или
![]()
где [K] - суммарная матрица жесткости системы;
{u} - вектор узловых перемещений;
{Fr} - вектор реактивных нагрузок;
{Fа} - суммарный вектор активных нагрузок;
![]() ,
,
где {Fnd} - вектор узловых нагрузок;
{Fepr} - вектор распределенного давления, прикладываемого к элементам.
Полученная система уравнений решалась "фронтальным" методом /1/.
1. Бате К., Вилсон Е. Численные методы анализа и метод конечных элементов/ Пер. с англ. А. С. Алексеева и др.; Под ред. А. Ф. Смирнова. – М.: Стройиздат, 1982 – 448 с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.