Проанализируем разность ![]() (1) в зависимости от значений
величин A,C и D=AC-B2:
(1) в зависимости от значений
величин A,C и D=AC-B2:
1) 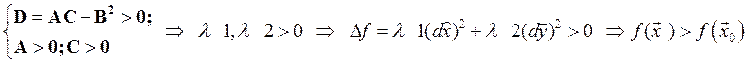 è
è
è стационарная точка х0 является точкой локального минимума.
2) 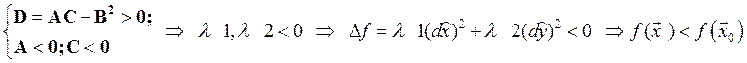 è
è
è стационарная точка х0 является точкой локального максимума.
3)D<0 ó собственные числа разного знака (например,![]() )ó в ПО(х0,r)
)ó в ПО(х0,r) ![]() (1)
принимает как положительные значения(
(1)
принимает как положительные значения(![]() в точках
прямой L1
в точках
прямой L1![]() ,
так и отрицательные значения (
,
так и отрицательные значения (![]() è стационарная точка х0
не является точкой локального экстремума функции.
è стационарная точка х0
не является точкой локального экстремума функции.
4)D=0
ó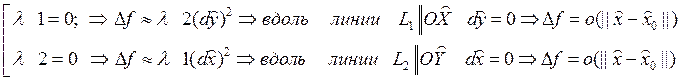
è формула Тейлора 2 порядка не достаточна для анализа стационарной точки х0.
Пример-1. Найти и исследовать стационарные точки функции f(x,y)=xy+x2+y3
1)Df(x,y)=[y+2x;x+3y2]=[0;0]ó (0;0);(-1/12; 1/6)
2)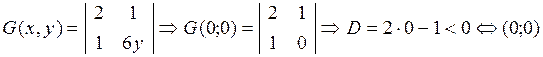 -не точка Л.Э.
G(-1/12;1/6)=
-не точка Л.Э.
G(-1/12;1/6)= 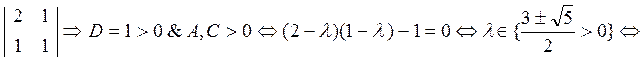 ó ст. точка (-1/12;1/6)- точка локального
минимума:
ó ст. точка (-1/12;1/6)- точка локального
минимума:
fmin=f(/1/12;1/6)=-1/(2×63).
Пример-2.
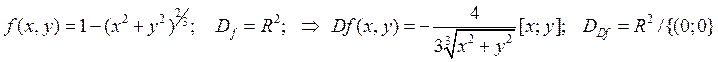
è стационарных точек функция не имеет, поэтому единственный «кандидат» в точки Л.Э. – точка (0;0): f непрерывна в точке и не существует Df(0;0).
Так как![]() , точка (0;0)-
точка Л.max.
, точка (0;0)-
точка Л.max.
Пусть f дифференцируемая функция . Методом "градиентного спуска"называют итерационный алгоритм отыскания (приближения к ) локального минимума Ф.Н.П., основанный на свойстве вектора v= - gradf(a), определяющего в каждой точке направление "наибыстрейшего убывания" функции.
Пусть извесно, что в некоторой окрестности точки ![]() имеется локальный минимум.
имеется локальный минимум.
Рассмотрим один "шаг" алгоритма метода "градиентного спуска".
1) Построим вектор ![]() и запишем уравнение луча L(прямой), проходящего через точку М в
направлении вектора
и запишем уравнение луча L(прямой), проходящего через точку М в
направлении вектора ![]() :
:![]() .
.
Значения функции в точках этого луча ![]() =φ(t) определяются одной переменной -
параметром "смещения" t.
=φ(t) определяются одной переменной -
параметром "смещения" t.
2) Выберем "шаг смещения " t0из условия убывания функции φ(t)
![]()
3) Перейдем в точку ![]() ,
значение функции в которой, очевидно,
,
значение функции в которой, очевидно, ![]()
Если в точке М1 ![]() ,
алгоритм работу заканчивает - точка М1- стационарная точка функции.
Если же
,
алгоритм работу заканчивает - точка М1- стационарная точка функции.
Если же ![]() , выполняется следующий шаг
алгоритма : по точке М1 находится точка М2 : f(М2)<f(М1).
, выполняется следующий шаг
алгоритма : по точке М1 находится точка М2 : f(М2)<f(М1).
Последовательность точек {xo,x1,..,xi,..} сходится к точке a : grad f(a) =0
Замечанмя. 1. На практике итерационный процесс прекращают, если ||grad[f(Mn)]||≤ eps.
2. Задача поиска максимума функции f, очевидно, сводится к задаче поиска минимума функции -f.
-------------------------------------------------------------------------------------------------------------------------
Пример. f(x,y) = x2 + 3y2 ; Mo(3,1) f(x,y) = [2x, 6y]t =2[x;3y]t; f(Mo)=12
I шаг]
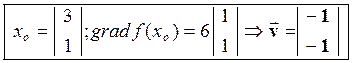
1) уравнение луча : 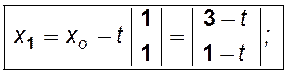
2) Сужение функции f на этот луч и ее стационарная точка to :
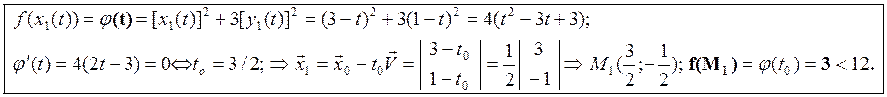
II] шаг
1) 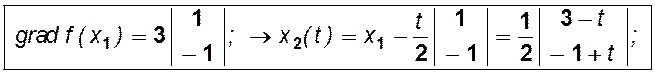
2) 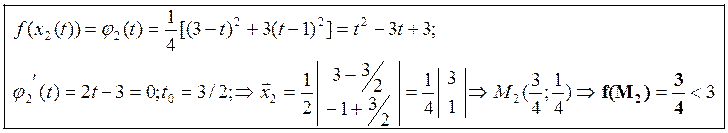
III] шаг 1) 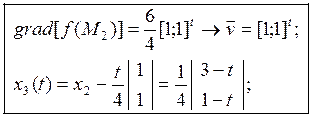
2) 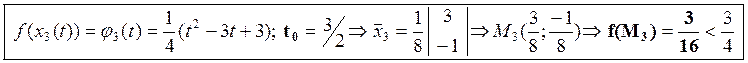
|
xi |
xo=[3, 1] |
x1=[3/2; -1/2] |
x2=[3/4; 1/4] |
x3=[3/8; -1/8] |
|
f(xi) |
12 |
3 |
3/4 |
3/16 |
|
|
6[1; 1] |
3[1;-1] |
3/2[1;1] |
3/4[1;-1] |
|
|
|
|
|
|
|
линия уровня
полуоси |
а=23; b=2 |
а=3; b=1 |
а=3/2; b=1/2 |
а=3/4; b=1/4 |
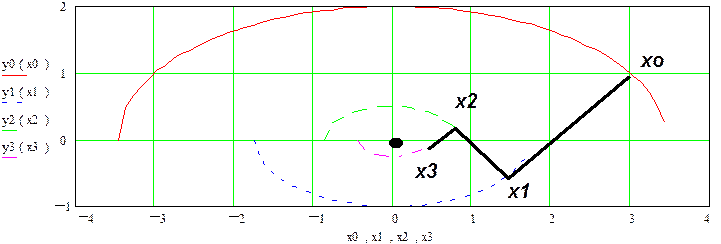
Обратите внимание : 1) f(xi)=12/4i ;
Vi=![]() /2i ; ai=23/2i; bi=2/2i ; q= 1/2 !!! линии уровня -
подобные эллипсы с полуосями, убывающими как геом.прогр. со знаменателем q.
/2i ; ai=23/2i; bi=2/2i ; q= 1/2 !!! линии уровня -
подобные эллипсы с полуосями, убывающими как геом.прогр. со знаменателем q.
Последовательность {xo,x1,x2,x3,...} сходится к точке (0,0) локального минимума.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.