Пример. f(x,y)=xexy; a=[1;2]. Df(x,y)=[exy(1+xy);x2exy]
è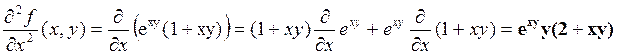
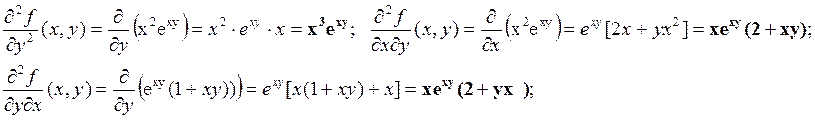
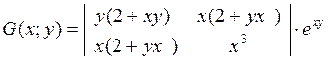
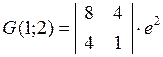
-------------------------------------------------------------------
Замечания.
2. Очевидно, что для функции “n” переменных определены “n” первых частных производных, “n2” – вторых,… “nк” частных производных порядка “k![]() ”.
”.
1. Df(x)- матрица-строка [1xn]; D2f(x) –двумерная матрица (таблица) [nxn]; D3f(x) – трехмерная (кубическая) таблица [nxnxn]:
 Например, для n=2 D3f(x,y)=
Например, для n=2 D3f(x,y)=![]() :
: 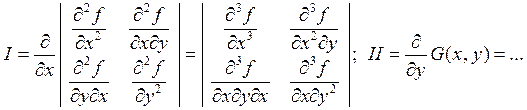
2. Очевидно, что для функции “n” переменных определены “n” первых частных производных, “n2” – вторых,… “nк” частных производных порядка “k![]() ”, из которых nk-n являются смешанными, причем часть из них различаются лишь порядком
дифференцирования, например,
”, из которых nk-n являются смешанными, причем часть из них различаются лишь порядком
дифференцирования, например, 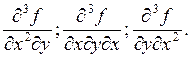
Теорема.(без док-ва). Непрерывные смешанные частные производные не зависят от порядка дифференцирования.
Следствие. Матрица Гессе G(a) дважды непрерывно
дифференцируемой ФНП является симметричной и имеет не более 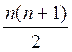 различных элементов. Например, для
f(x,y)=xexy
различных элементов. Например, для
f(x,y)=xexy 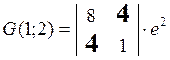
Пусть функция f непрерывна в точке ![]()
Сравним значения f(a) и f(![]() ПО(а,r)).
ПО(а,r)).
Определение 1.
Если ![]() , точка а
называется точкой локального минимума функции;
, точка а
называется точкой локального минимума функции;
Если ![]() , точка а
называется точкой локального максимума функции.
, точка а
называется точкой локального максимума функции.
Определение 2. Точка а=[a1,..,ai,..,an]tдифференцируемой функции f называется
стационарной, если 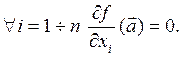
Пусть точка а является точкой
локального экстремума (т.л.э.) ФНП f. Из определения 1 (![]() следует, что точка “ai” функции одной переменной
следует, что точка “ai” функции одной переменной ![]() так же является т.л.э.
и следовательно: либо
так же является т.л.э.
и следовательно: либо ![]() , либо
, либо ![]()
Таким образом, из определений 1,2 и
определения 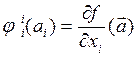 следует
следует
Необходимый признак локального экстремума непрерывной ФНП: частные производные ФНП в точке либо равны нулю, либо не существуют.
Геометрически для функции двух переменных локальный
экстремум связан с касательной плоскостью к непрерывной в точке А(аx,ay,f(ax,ay))поверхности z=f(x,y): если касательная плоскость в точке существует, она горизонтальна (![]() ) и поверхность в ПО(а,r) расположена выше или ниже ее;
) и поверхность в ПО(а,r) расположена выше или ниже ее;
либо касательная плоскость в точке не существует.
Например, вершина А(0,0,0) конической поверхности
соответствует минимуму функции ![]() и в А не
существует касательной плоскости.
и в А не
существует касательной плоскости.
В точке А(0,0,1) верхней полусферы ![]() касательная плоскость z=1 горизонтальна и функция
касательная плоскость z=1 горизонтальна и функция ![]() достигает в точке максимума fmax=f(0,0)=1.
достигает в точке максимума fmax=f(0,0)=1.
Важное замечание. Дифференцируемая функция достигает локального экстремума только в стационарной точке, но не всякая ст. точка является точкой локального экстремума.
Пусть в точке а функция ![]() имеет непрерывные вторые
частные производные ó
имеет непрерывные вторые
частные производные ó
![]()
Теорема (без док-ва).Если ФНП имеет непрерывные вторые частные производные в точке а, в некоторой окрестности этой точки имеет место формула Тейлора 2 порядка:
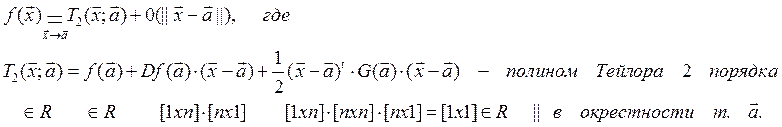
Для функции двух переменных f(x,y) и точки ![]()
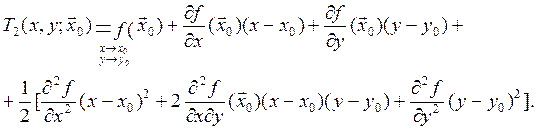
Если точка х0 - стационарная точка функции (Df(х0)=[0,0]), разность значений функции в достаточно малой окрестности точки xèx0
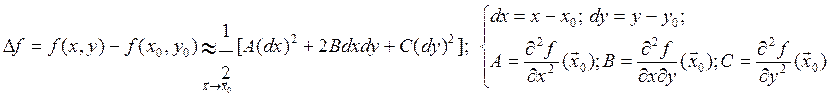
определяется квадратичной формой, причем матрица
квадратичной формы – симметричная матрица Гессе 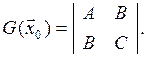
Из линейной алгебры известно, что в прямоугольной
системе координат ![]() , определяемой собственными
векторами
, определяемой собственными
векторами ![]() матрицы:
матрицы:
![]() , квадратичная форма имеет
канонический вид
, квадратичная форма имеет
канонический вид
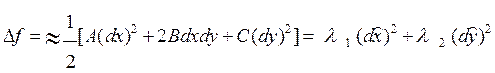 ,
(1)
,
(1)
причем собственные числа ![]() матрицы
G(a) являются решениями уравнения
матрицы
G(a) являются решениями уравнения
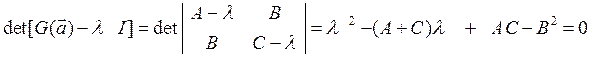 (2) и по теореме Виета:
(2) и по теореме Виета: 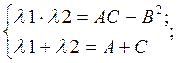
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.