Следствие. Если функция f дифференцируема в точке а, то:
1. в точке а существуют все ее частные производные;
2. при хèa имеет место формула
Тейлора 1 порядка
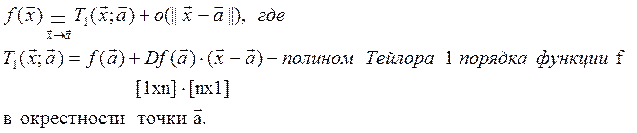
Докажем для n=2 –f дифф. функция двух переменных:
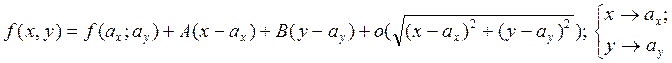
1)Рассмотрим «частный» предел вдоль прямой Lx ||OX:y=ay=const; xèax:
![]()
![]()
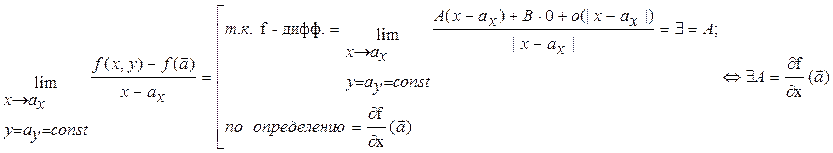
Аналогично докажем, что 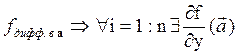
2) Подставив найденные значения А и В, получим:
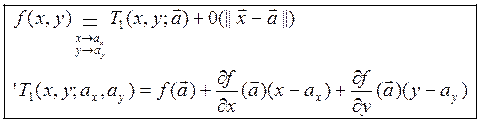
Определение 2. Поверхность в R3, задаваемая дифференцируемой функцией двух переменных f(x,y), называется гладкой поверхностью.
«Воспоминания» из аналитической геометрии.
Плоскость α задается в R3 точкой M0(x0,y0,z0) и нормальным вектором 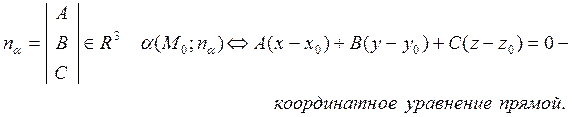
Прямая l задается в R3 точкой M0(x0,y0,z0) и направляющим вектором
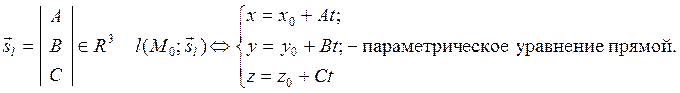
Пусть z=f(x,y)- гладкая поверхность и M0(x0,y0,z0=f(x0,y0))- точка на этой поверхности.
Запишем полином Тейлора 1 порядка для
функции f в окрестности точки М0
: 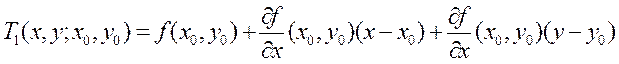
Очевидно, что уравнение z=T1(x,y;x0,y0) определяет в R3 плоскость
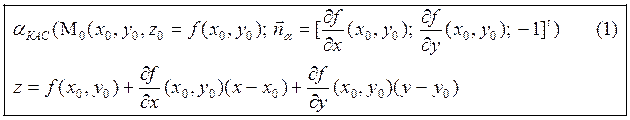 , которая проходит через точку
поверхности M0(x0,y0,z0=f(x0,y0)).
, которая проходит через точку
поверхности M0(x0,y0,z0=f(x0,y0)).
Определение 3. Плоскость (1) называется касательной плоскостью к гладкой поверхности z-f(x,y) в точке М0.
Определение 4. Прямая l(M0;Sl=nά):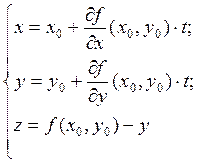 проходящая
через точку М0 поверхности и перпендикулярная касательной плоскости
называется нормалью к поверхности в точке М0.
проходящая
через точку М0 поверхности и перпендикулярная касательной плоскости
называется нормалью к поверхности в точке М0.
Пример. f(x,y)= xexy; x0=[1,2]t; M0(1,2,e2).
T1(x,y;1,2)=e2+3e2(x-1)+e2(y-2) – полином Тейлора 1 порядка;
z=xexy – гладкая поверхность;
![]() e2[1+3(x-1)+(y-2)]- касат. плоскость
e2[1+3(x-1)+(y-2)]- касат. плоскость
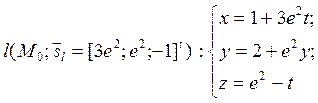 - нормаль к поверхности в
точке М0.
- нормаль к поверхности в
точке М0.
!!! В дальнейшем будем отождествлять дифференцируемость ФНП в точке a€Rn, формулу и полином Тейлора 1 порядка в окрестности точки а и существование касательной плоскости и нормали к гладкой поверхности в точке M(a,f(a)): fдифф(a) ó f(x)=f(a)+Df(a)(x-a)+o(||x-a||) ó αКАС(M;nα=[Df(a);-1]t; lN(M;Sl=nα).
«Предисловие… из прошлого».
·
Если ![]() то
то 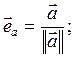 - соответствующий единичный вектор (
- соответствующий единичный вектор (![]() ) и
) и![]() .
.
·
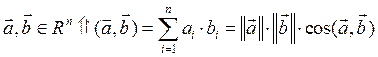 -скалярное произведение векторов.
-скалярное произведение векторов.
Пусть ФНП f дифференцируема в точке а![]() и задан
вектор
и задан
вектор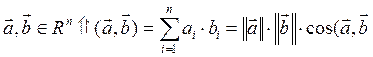 , определяющий в точке а
некоторое направление.
, определяющий в точке а
некоторое направление.
Запишем для точки ![]() формулу Тейлора 1 порядка:
формулу Тейлора 1 порядка:
![]()
Определение 1. Производной ФНП f в точке а в направлении L называется число
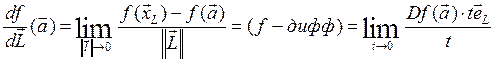
равное скалярному произведению градиента функции в точке на вектор направления, деленному на норму этого вектора.
Следствия.
1. Модуль 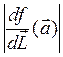 определяет «скорость изменения»
функции f в точке в заданном
направлении, при этом величина скорости равна
определяет «скорость изменения»
функции f в точке в заданном
направлении, при этом величина скорости равна ![]()
2. Если 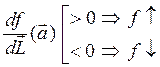 в точке в направлении L.
в точке в направлении L.
3. Так как наиб.{|cos|}=cos(o)=1, функция f с наибольшей скоростью
возрастает в направлении ![]() и убывает в направлении
и убывает в направлении ![]()
Пример. f(x,y)=xexy; a=[1;2]t; L=[1;1]t.
è gradf(a)=e2[3;1]t; 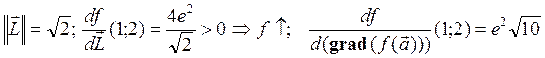
---------------------------------------------------------------------------
Пусть ФНП f дифференцируема в области ![]() и непрерывны
все ее частные производные функции “n” переменных
и непрерывны
все ее частные производные функции “n” переменных 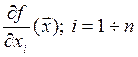 , для каждой из которых
определены ее частные производные.
, для каждой из которых
определены ее частные производные.
Определение 1. Частную производную 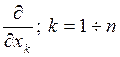 функции
функции 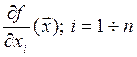 называют второй частной
производной ФНП и пишут:
называют второй частной
производной ФНП и пишут:
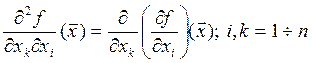
Например, для функции n=2 переменных таким образом определены 4 вторые частные
производные: 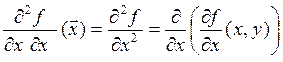 («дэ два эф по дэ икс
дважды»);
(«дэ два эф по дэ икс
дважды»);
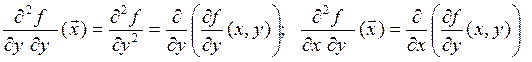 («дэ два эф по
дэ икс дэ игрек»);
(«дэ два эф по
дэ икс дэ игрек»); 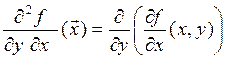 .
.
Определение 2. Квадратная матрица порядка “n”, составленная из вторых частных
производных ФНП, называется матрицей Гессе 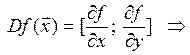
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.